You're using an outdated browser. Please upgrade to a modern browser for the best experience.
Please note this is a comparison between Version 1 by Azadeh Famili and Version 2 by Lindsay Dong.
Machine learning deployment on edge devices has faced challenges such as computational costs and privacy issues. Membership inference attack (MIA) refers to the attack where the adversary aims to infer whether a data sample belongs to the training set. In other words, user data privacy might be compromised by MIA from a well-trained model. Therefore, it is vital to have defense mechanisms in place to protect training data, especially in privacy-sensitive applications such as healthcare.
- membership inference attack
- defense
- MIA
1. Introduction
Machine learning is an evolving field that has recently gained significant attention and importance. With the exponential growth of data and advancements in computing power, machine learning has become a powerful tool for extracting valuable insights, making predictions, and automating complex tasks. Significant advancements in machine learning have led to the remarkable performance of neural networks in a wide range of tasks [1][2][1,2]. As the demand for real-time processing and low-latency applications continues to rise, the importance of efficient hardware implementations of machine learning algorithms becomes evident. Hardware acceleration plays a crucial role in meeting the computational requirements and enabling the deployment of machine learning models in resource-constrained environments.
To facilitate the efficient deployment of machine learning models on hardware platforms, scientists and researchers have proposed compression techniques to accelerate training and inference processes. To this end, one of the promising techniques in model compression is quantization. Quantization methods [3][4][5][3,4,5] accelerate the computation by executing the operations with reduced precision. These methodologies have achieved performance levels comparable to those of full bitwidth networks while remaining compatible with resource-constrained devices. These methods also enable broader possibilities for machine learning applications, particularly in sectors that handle sensitive data on the edge.
This approach also proves valuable in various use cases, such as medical imaging [6], autonomous driving [7], facial recognition [8], and natural language processing [2], where the data privacy is of utmost importance. However, as these technologies become increasingly intertwined with daily life, they must be continuously evaluated for vulnerabilities and privacy concerns. For example, as shown in Figure 1, patient data can be used to train neural networks. In most cases, hospitals or healthcare providers gather a large amount of data regarding patients’ identity, health, insurance, and finance information. An adversary may attempt to gain access to this information at every step of this process, compromising user data privacy in machine learning applications.
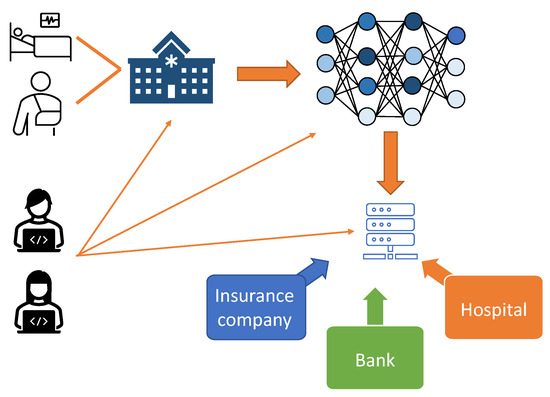
Figure 1. A patient medical and personal information is valuable in the field of machine learning. An adversary can jeopardize patient privacy from the machine learning models that are trained on the data.
2. Quantization Methods of Defense against Membership Inference Attacks
The issue of privacy attacks in neural network training applications has raised significant concerns, particularly in sensitive scenarios [9][18]. Extensive research has been conducted to address the privacy implications associated with training data, focusing on various aspects such as data leakage, prevention of memorization, and evaluation of the privacy efficacy of proposed defense mechanisms. Among these, MIA has emerged as a critical concern to user data privacy in machine learning applications, as it has been shown that MIA can effectively determine whether a data sample belongs to the training set. Such MIA methods are able to extract the user data information contained in the overparameterized model. The high-level overview of MIA is shown in Figure 2. An adversary passes a data sample x to the target model using some analysis tools to determine the membership of this data sample.
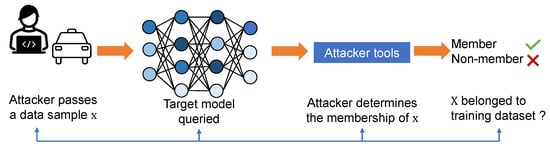
Figure 2.
Overview of MIA attack. Here x is a data sample which the attacker wants to determine its membership.
The first MIA approach [10][19] uses shadow models that are trained on the same (or a similar) distribution as the training data. The method assigns membership to input and constructs a new dataset to train the classifier. Subsequently, various MIA attacks were developed considering different threat models and application scenarios. The work in [11][20] proves that when the adversary has data from a different but similar task, the shadow models are not needed, while a threshold reaching max prediction confidence can provide satisfactory results. The results in [12][21] find that the training process of ML models is the key to implementing a successful MIA. As the goal is to minimize losses associated with the training samples, members in general tend to have smaller losses than non-member samples. It has been shown that the effectiveness of MIA can be improved by using inputs from query methods [13][22]. The vulnerability of adversarially trained models to MIA attacks has also been exploited [14][23].
2.1. Model Quantization
Quantization methods have been shown to be promising in reducing the memory footprint, computational complexity, and energy consumption of neural networks. They focus on converting floating-point numbers into representations with lower bitwidth. For example, quantization can be used to reduce the model size by converting all the parameters’ precision from 32 bits to 8 bits or lower for achieving a higher compression rate or acceleration [15][24]. Extreme quantization is also possible where the model weights can be binary [16][25] or ternary [17][26]. In general, quantization methods can be divided into three categories. Traditional quantization. In these methods, all weights and activations would be quantized. For instance, a non-uniform quantization method uses reduced bitwidth for the majority of data while a small amount of data are handled with high bitwidth [18][27]. A different approach in the same category utilizes a quantizer that dynamically adapts to the distribution of the parameters [19][28]. A quantization algorithm is developed by approximating the gradient to the quantizer step size, which can perform comparably to the full bitwidth model [20][29]. In [21][30], the proposed quantization function is a linear combination of several sigmoid functions with learnable biases and scales. The method proposed in [16][25] restricts weights and activations to binary values (−1,1) , enabling further reduction in memory footprint and efficient hardware implementation. A more stringent quantization method uses three levels (−1,0,1) to represent weights and activations, striking a balance between binary quantization and full bitwidth. Mixed-precision quantization. To avoid performance deterioration, some studies suggest using mixed-precision quantization instead of compressing all the layers to the same bidwidth. Mixed-precision quantization typically involves dividing the network into layers or blocks and applying different bitwidths to each part based on its importance and sensitivity to quantization. For example, the quantization bitwidths can be obtained by exploiting second-order (Hessian matrix) information [22][31]. Differentiable architecture search is also employed by [23][24][32,33] to perform mixed-precision quantization. Dynamic inference quantization. Dynamic inference quantization offers several benefits, including improved flexibility, enhanced adaptability to varying run-time conditions, and potentially better accuracy than quantization with fixed bitwidth. By adjusting the quantization bitwidth on the fly, dynamic inference quantization enables efficient deployment of deep neural network models in resource-constrained environments without sacrificing accuracy. To this end, one approach is to use a bit-controller trained jointly with the given neural network for dynamic inference quantization [25][34]. Another study [26][35] proposes dynamically adjusting the quantization interval based on time step information. An algorithm developed by [27][36] detects sensitive regions and proposes an architecture that employs a flexible variable-speed mixed-precision convolution array.2.2. Defense against MIA
A defense mechanism against MIA, named MemGuard, was developed [28][42], which can evade the attacker’s membership classification and transform the prediction scores into an adversarial example. MemGuard adds a carefully crafted noise vector to the prediction vector and turns it into an adversarial example of the attack model. Differential privacy [29][30][43,44], which can provide a probabilistic guarantee of privacy, has also been shown to be effective in enhancing resistance against MIA [31][37]. However, differential privacy is costly to implement, and the accuracy reduction makes the method impractical. Distillation for membership privacy (DMP) is a method proposed by [32][38]. DMP first trains a teacher model and uses it to label data records in the unlabeled reference dataset. The teacher method has no defense mechanism. DMP requires a private training dataset and an unlabeled reference dataset. The purifier framework [33][39], where the confidence scores of the target model are used as input and are purified by reducing the redundant information in the prediction score, has also been proposed to defend against MIA. On the other hand, regularization methods designed to reduce overfitting in machine learning models can be employed as defense strategies against MIAs. Adversarial regularization [34][40] and Mixup + MMD [35][41] are specific regularization techniques intended to mitigate MIAs. Using regularization, the model generalization is improved and the gap between member and non-member data samples is reduced. Table 1 summarized prior work based on attack knowledge, MIA attack, and defense mechanism.Table 1.
Prior of each table appears in numerical order. research on defense against MIA.
| Reference | Attack Knowledge | Corresponding Attack | Defense Mechanism | |
|---|---|---|---|---|
| 1 | [31][37] | Black-box | Shadow training | Differential privacy |
| 2 | [32][38] | Black-box and White-box | Classifier based and Prediction loss | Distillation |
| 3 | [33][39] | Black-box | Classifier based and Prediction correctness | Prediction purification |
| 4 | [34][40] | Black-box | Shadow training | Regularization |
| 5 | [35][41] | Black-box | Shadow training | Regularization |
| 6 | [28][42] | Black-box | Classifier based | MemGuard |
