Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 3 by Lindsay Dong and Version 2 by Lindsay Dong.
Flow-shop scheduling problems are classic examples of multi-resource and multi-operation scheduling problems where the objective is to minimize the makespan. Because of the high complexity and intractability of the problem, apart from some exceptional cases, there are no explicit algorithms for finding the optimal permutation in multi-machine environments.
- flow-shop
- scheduling problem
- algorithm
1. Introduction
Scheduling problems, in general, have been extensively studied across a wide range of domains due to their relevance for optimizing resource allocation, improving productivity, and reducing operational costs. Efficient scheduling has a direct impact on overall system performance, making it a critical area of research in operations management and industrial engineering. Flow-shop scheduling belongs to the broader class of multi-resource and multi-operation scheduling problems. With all its variants, it belongs to the class of NP-hard problems, which are known to have no polynomial time solution method. As a matter of course, small tasks or very special cases may be handled in reasonable time, but in general these problems are intractable. Obviously, the time complexity of finding a good solution in a shorter time may essentially effect the efficiency and the costs of real industrial and logistics applications. Alas, in such problems, the complexity increases exponentially in terms of the number of jobs, machines, and processing steps involved. Additionally, the presence of parallel machines and precedence constraints further complicates the optimization process. These challenges make it computationally infeasible to find optimal solutions for large-scale instances, necessitating the adoption of heuristic and metaheuristic methods. Apart from some exceptional cases, there are no explicit algorithms for finding the optimal permutation in multi-machine environments. Therefore, different heuristic approaches and evolutionary algorithms are used to calculate solutions that are close to the optimal solution. Evolutionary and population-based algorithms, inspired by the principles of natural selection and geneticsor by the behavior of groups of animals have demonstrated rather good efficiency at solving various optimization problems, including flow-shop scheduling.
2. The Flow-Shop Problem
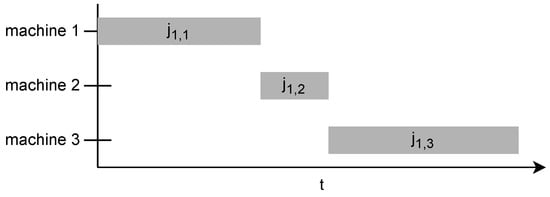
Flow-shop scheduling for manufacturing is a production planning and control technique used to optimize the sequence of operations that each job must undergo in a manufacturing facility. In a flow-shop environment, multiple machines are arranged in a specific order, and each job must pass through the same sequence of operations on these machines. The objective of flow-shop scheduling is to minimize the total time required to complete all jobs (makespan) or to achieve other performance measures such as minimizing the total completion time, total tardiness, or maximizing resource utilization. The storage buffer between machines is considered to be infinite. If the manufactured products are small in physical size, it is often easy to store them in large quantities between operations [1]. Permutation flow shop is a specific type of flow-shop scheduling problem in manufacturing where a set of jobs must undergo a predetermined sequence of operations on a series of machines. In the permutation flow shop, the order of operations for each job remains fixed throughout the entire manufacturing process. However, the order in which the jobs are processed on the machines can vary, resulting in different permutations of jobs [2]. Consider a flow-shop environment, where 𝑁𝐽 denotes the number of jobs and 𝑁𝑅 is the number of resources (machines). A given permutation , where i is the index of the job, 𝑝𝑗𝑖,𝑟 represents the processing times, is the rth resource in the manufacturing line, is the starting times of job on machine r, and is the completion time of job on resource r, has the following constraints: A resource can only process one job at a time; therefore, the start time of the next job must be equal to or greater than the completion time of its predecessor on the same resource: A job can only be present on one resource at a given time; therefore, the start time of the same job on the next resource must be greater then or equal to the completion time of its preceding operation: The first scheduled job does not have to wait for other jobs and is available from the start. The completion time of the first job on the current machine is the sum of its previous operations on preceding machines in the chain and its processing time on the current machine: Figure 1 shows how the first scheduled job has only one contingency: its own operations on previous machines.
Figure 1. Example of the first job not waiting.
Jobs on the first resource are only contingent on jobs on the same resource; therefore, the completion time of the job is the sum of the processing times of previously scheduled jobs and its own processing time:
Figure 2 shows how there is only on contingency on the first machine; therefore, operations can follow each other without downtime.


Figure 2. Example of jobs on the first machine.
When it comes to subsequent jobs on subsequent machines, the completion times depend on the same job on previous machines (Equation (2)) and previously scheduled jobs on previous machines in the chain (Equation (1)):
Figure 3 shows the contingency of jobs. is contingent upon and , where it has to wait for to finish despite the availability of machine 2. 𝑗2,3 is contingent upon and , where it has to wait for machine 3 to become available despite being completed on machine 2.
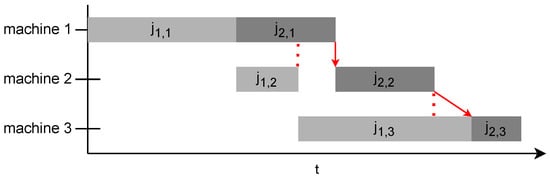

Figure 3. Contingency of start times.
The completion time of the last job on the last resource is to be minimized and is called the makespan.
One of the most widely used objective function is to minimize the makespan:
Figure 4 illustrates how the completion time of the last scheduled job on the last machine in the manufacturing chain determines the makespan.
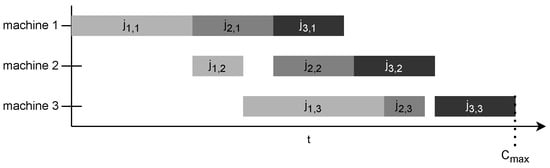

Figure 4. Example for obtaining 𝐶𝑚𝑎𝑥.
3. Classic and State-of-the-Art Approaches
3.1. Classic Approaches
One of the most referenced algorithms is the NEHT (or NEH-Tailard) algorithm. It is based on the Nawaz–Enscore–Ham (NEH) algorithm [3] The NEH algorithm has been widely studied and used in various fields, including manufacturing, operations research, and scheduling problems. While it may not always find the optimal solution, it usually provides good-quality solutions in a reasonable amount of time, making it a practical and efficient approach for solving permutation flow-shop scheduling problems. The NEHT algorithm is improved by Taillard [4]. The NEH-Tailard algorithm works similarly to the NEH algorithm but incorporates a different way of inserting jobs into the sequence. While the original NEH algorithm used the “insertion strategy” to determine the position for each job insertion, Tailard introduced a “tie-breaking” rule to break the ties between jobs with equal makespan values during the insertion process. By carefully selecting the order of job insertion, Tailard aimed to find better solutions and potentially improve the quality of the resulting schedules. The NEH-Tailard algorithm has shown to outperform the original NEH algorithm and has been widely cited in scheduling research as a more efficient and effective approach to solving permutation flow-shop scheduling problems.3.2. Heuristic or Meta-Heuristic Algorithms
The simulated annealing (SA) [5] algorithm is a classic pseudo-random search algorithm, inspired by the annealing process in metallurgy. It is commonly used to solve combinatorial optimization problems, especially those with a large search space and no clear gradient-based approach to finding the global optimum. The algorithm is named after the annealing process used in metallurgy, where a metal is heated to a high temperature and then gradually cooled to reduce defects and obtain a more stable crystal structure. Similarly, simulated annealing starts with a high “temperature” to allow the algorithm to explore a wide range of solutions and then gradually decreases the temperature over time to converge towards a near-optimal solution, which can produce satisfactory results for flow-shop scheduling problems [6]. The key feature of simulated annealing is the acceptance of worse solutions with decreasing probability as the temperature decreases. This enables the algorithm to explore the search space broadly in the early stages and gradually converge towards a better solution as the temperature cools down. By incorporating stochastic acceptance of worse solutions, simulated annealing is able to escape local optima and has the potential to find near-optimal solutions for complex optimization problems. There are simulated annealing based scheduling algorithms like [6][7][8][9][10][11] Particle swarm optimization (PSO) describes a group of optimization algorithms where the candidate solutions are particles that roam the search space iteratively. There are many PSO variants. The particle swarm optimization 1 (PSO1) algorithm is a PSO that uses the smallest position value (SPV) [12] heuristic approach and the VNS [13] algorithm to improve the generated permutations [14]. The particle swarm optimization 2 (PSO2) algorithm is a simple PSO algorithm proposed by Ching-Jong Liao [15]. This approach introduces a new method to transform the particle into a new permutation. The combinatorial particle swarm optimization (CPSO) algorithm improves the simple PSO algorithm to optimize for integer-based combinatorial problems. Its characteristics differ from the standard PSO algorithm in each particle’s definition and speed, and in the generation of new solutions [16]. The hybrid adaptive particle swarm optimization (HAPSO) algorithm uses an approach that optimizes every parameter of the PSO. The velocity coefficients, iteration count of the local search, upper and lower bounds of speed, and particle count are optimized during runtime, resulting in a new efficient adaptive method [17]. The PSO with expanding neighborhood topology (PSOENT) algorithm uses the neighborhood topology of a local and a global search algorithm. First, the algorithm generates two neighbours for every particle. The number of neighbours increases every iteration until it reaches the number of particles. If the termination criteria are not met, every neighbour is reinitialized. The search ends when the termination criteria are met. These steps ensure that no two consecutive iterations have identical neighbour counts. This algorithm relies on two meta-heuristic approaches: variable neighborhood search (VNS) [13] and path relinking (PR) [18][19]. VNS is used to improve the solutions of each particle, while the PR strategy improves the permutation of the best solution [20]. The ant colony optimization (ANS) [21] algorithm is a virtual ant colony-based optimization approach introduced by Marco Dorigo in 1992 [22][23]. Hayat et al., in 2023 [24], introduced a new hybridization of particle swarm optimization (HPSO) using variable neighborhood search and simulated annealing to improve search results further.3.2.1. Approaches Based on Genetic Algorithms
The simple genetic algorithm (SGA) is a standard genetic algorithm. It is similar to the self-guided genetic algorithm (SGGA), except it is not expanded with a probability model [25]. The mining gene genetic algorithm (MGGA) was explicitly developed for scheduling resources. The linear assignment algorithm and the greedy heuristics are all built-in [25]. The artificial chromosome with genetic algorithms (ACGA) is a newfound approach. It combines an EDA (estimation of distribution approach) [26][27][28][29] with a conventional algorithm. The probability model and the genetic operator generate new solutions and differ from the SGGA [25]. The self-guided genetic algorithm (SGGA) belongs to the category of EDAs. Most EDAs use the probability model explicitly to search for new solutions without using genetic operators. They realized that global statistics and local sets of information must amend one another. The SGGA is a unique solution for combining these two types of information. It does not use a probability model but predicts each solution’s fitness. This way, the mutational and crossover operations can produce better solutions, increasing the algorithm’s efficiency [25]. Storn and Prince introduced the differential equation (DE) algorithm in 1995 [30]. Like every genetic algorithm, the DE is population-based. Floating-point-based chromosomes represent every solution. Traditional DE algorithms are unable to optimize discrete optimization problems. Therefore, they introduced the discrete differential equation (DDE) [14][31][32] algorithm, in which each solution represents a discrete permutation. In the DDE, a job’s permutation represents each individual. Since every permutation is treated stochastically, scholars treat every solution uniquely [32]. The genetic algorithm with variable neighborhood search (GAVNS) is a genetic algorithm that utilizes the VNS [13] local search [33]. Mehrabian and Lucas introduced the invasive weed optimization (IWO) algorithm in 2006 [34]. It is based on a common agricultural phenomenon: spreading invasive weeds. It has a straightforward, robust structure with few parameters. As a result, it is easy to comprehend and implement [35]. The hybrid genetic simulated annealing (HGSA) algorithm uses the local search capabilities of the simulated annealing (SA) algorithm and integrates it with a genetic algorithm. This way, the quality of the solutions and the runtimes are improved [36]. The hybrid genetic algorithm (HGA) differs from the simple genetic algorithm by incorporating two local search algorithms. The genetic algorithm works on the whole domain as a global search algorithm. Furthermore, it uses an orthogonal-array-based crossover (OA-crossover) to increase efficiency [37]. The hormone modulation mechanism flower pollination algorithm (HMM-FPA) is a flower pollination-based algorithm. Flowers represent each individual in the population; pollination occurs between them. They can also self-pollinate, representing closely packed flowers of the same species [38].3.2.2. DBMEA-Based Approaches
The simple discrete bacterial memetic evolutionary algorithm (DBMEA) is a specific variant of the memetic algorithm used for optimization problems. Memetic algorithms combine elements of both evolutionary algorithms (EAs) and local search to efficiently explore the solution space and find high-quality solutions. The “Bacterial” aspect in DBMEA is inspired by the behavior of bacteria in nature. The algorithm uses a population-based approach where each candidate solution (individual) is represented as a “bacterium”. These bacteria evolve over generations using mechanisms similar to those found in evolutionary algorithms, such as selection, crossover, and mutation. The “memetic” aspect indicates that each bacterium undergoes a local search process to improve its quality within its neighborhood. This local search is typically a problem-specific optimization procedure that helps the algorithm fine-tune the solutions locally. The “discrete” in DBMEA suggests that the problem domain is discrete in nature, meaning that the variables or components of the solution are discrete and not continuous. According to the investigations, it could not generate satisfactory results based on the Taillard [4] benchmark results. Therefore, scholars combined it with other algorithms, producing hybrid solutions that use the DBMEA as a global search algorithm. The discrete bacterial memetic evolutionary algorithm with simulated annealing (DBMEA + SA) [39] uses the simulated annealing as a local search algorithm, while the DBMEA poses as a global search algorithm to walk the domain space similar to genetic algorithms.3.2.3. Jaya-Based Approaches
The Jaya optimization algorithm is a parameter-less optimization technique that does not require the tuning of any specific parameters or control variables. Its simplicity and ability to strike a balance between exploration and exploitation make it effective at solving various optimization problems. It may not guarantee a global optimum, but it often converges to good-quality solutions in a reasonable amount of time for many real-world applications. In 2022, Alawad et al. [40] introduced a discrete Jaya algorithm (DJRL3M) for FSSP that improved its search results using refraction learning and three mutation methods. This method is an improvement over the discrete Jaya (DJaya) algorithm proposed by Gao et al. [41].3.2.4. Social Engineering Optimizer
A social engineering optimizer (SEO) is described as a new single-solution meta-heuristic algorithm inspired by the social engineering (SE) phenomenon and its techniques. In SEO, each solution is treated as a counterpart to a person, and the traits of each person (e.g., one’s abilities in various fields) correspond to the variables of each solution in the search space. Ref. [42] introduces a novel sustainable distributed permutation flow-shop scheduling problem (DPFSP) based on a triple bottom line concept. A multi-objective mixed integer linear model is developed, and to handle its complexity, a multi-objective learning-based heuristic is proposed, which extends the social engineering optimizer (SEO).3.2.5. Hybrid Approaches
In [43], the authors tackle the flow-shop scheduling problem (FSSP) on symmetric networks using a hybrid optimization technique. The study combines the strengths of ant colony algorithm (ACO) with particle swarm optimization (PSO) to create an ACO-PSO hybrid algorithm. By leveraging local control with pheromones and global maximum search through random interactions, the proposed algorithm outperforms existing ones in terms of solution quality. The ACO-PSO method demonstrates higher effectiveness, as validated through computational experiments. Addressing the NP-hard nature of flow-shop scheduling problems, ref. [44] presents a computational efficient optimization approach called NEH-NGA. The approach combines the NEH heuristic algorithm with the niche genetic algorithm (NGA). NEH is utilized to optimize the initial population, three crossover operators enhance genetic efficiency, and the niche mechanism controls population distribution. The proposed method’s application on 101 FSP benchmark instances shows significantly improved solution accuracy compared to both the NEH heuristic and standard genetic algorithm (SGA) evolutionary meta-heuristic. Ref. [45] addresses the flexible flow-shop scheduling problem with forward and reverse flow (FFSPFR) under uncertainty using the red deer algorithm (RDA). The study employs the Fuzzy Jiménez method to handle uncertainty in important parameters. The authors compare RDA with other meta-heuristic algorithms, such as the genetic algorithm (GA) and imperialist competitive algorithm (ICA). The RDA performs the best at solving the problem, achieving near-optimal solutions in a shorter time than the other algorithms.References
- Pinedo, M. Scheduling: Theory, Algorithms, and Systems, 5th ed.; Springer: Cham, Switzerland, 2016.
- Johnson, S.M. Optimal two-and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–68.
- Nawaz, M.; Enscore, E.E., Jr.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95.
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285.
- Van Laarhoven, P.J.; Aarts, E.H. simulated annealing. In Simulated Annealing: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 1987; pp. 7–15.
- Dai, M.; Tang, D.; Giret, A.; Salido, M.A.; Li, W.D. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm. Robot. Comput.-Integr. Manuf. 2013, 29, 418–429.
- Jouhari, H.; Lei, D.; A. A. Al-qaness, M.; Abd Elaziz, M.; Ewees, A.A.; Farouk, O. Sine-Cosine Algorithm to Enhance simulated annealing for Unrelated Parallel Machine Scheduling with Setup Times. Mathematics 2019, 7, 1120.
- Alnowibet, K.A.; Mahdi, S.; El-Alem, M.; Abdelawwad, M.; Mohamed, A.W. Guided Hybrid Modified simulated annealing Algorithm for Solving Constrained Global Optimization Problems. Mathematics 2022, 10, 1312.
- Suanpang, P.; Jamjuntr, P.; Jermsittiparsert, K.; Kaewyong, P. Tourism Service Scheduling in Smart City Based on Hybrid Genetic Algorithm simulated annealing Algorithm. Sustainability 2022, 14, 6293.
- Redi, A.A.N.P.; Jewpanya, P.; Kurniawan, A.C.; Persada, S.F.; Nadlifatin, R.; Dewi, O.A.C. A simulated annealing Algorithm for Solving Two-Echelon Vehicle Routing Problem with Locker Facilities. Algorithms 2020, 13, 218.
- Rahimi, A.; Hejazi, S.M.; Zandieh, M.; Mirmozaffari, M. A Novel Hybrid simulated annealing for No-Wait Open-Shop Surgical Case Scheduling Problems. Appl. Syst. Innov. 2023, 6, 15.
- Bean, J.C. Genetic algorithms and random keys for sequencing and optimization. ORSA J. Comput. 1994, 6, 154–160.
- Hansen, P.; Mladenović, N. Variable neighborhood search: Principles and applications. Eur. J. Oper. Res. 2001, 130, 449–467.
- Tasgetiren, M.F.; Liang, Y.C.; Sevkli, M.; Gencyilmaz, G. A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem. Eur. J. Oper. Res. 2007, 177, 1930–1947.
- Liao, C.J.; Tseng, C.T.; Luarn, P. A discrete version of particle swarm optimization for flowshop scheduling problems. Comput. Oper. Res. 2007, 34, 3099–3111.
- Jarboui, B.; Ibrahim, S.; Siarry, P.; Rebai, A. A combinatorial particle swarm optimisation for solving permutation flowshop problems. Comput. Ind. Eng. 2008, 54, 526–538.
- Marchetti-Spaccamela, A.; Crama, Y.; Goossens, D.; Leus, R.; Schyns, M.; Spieksma, F. Proceedings of the 12th Workshop on Models and Algorithms for Planning and Scheduling Problems. 2015. Available online: https://feb.kuleuven.be/mapsp2015/Proceedings%20MAPSP%202015.pdf (accessed on 23 August 2023).
- Glover, F.; Laguna, M.; Marti, R. Scatter search and path relinking: Advances and applications. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2003; pp. 1–35.
- Resende, M.G.; Ribeiro, C.C.; Glover, F.; Martí, R. Scatter search and path-relinking: Fundamentals, advances, and applications. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 87–107.
- Marinakis, Y.; Marinaki, M. Particle swarm optimization with expanding neighborhood topology for the permutation flowshop scheduling problem. Soft Comput. 2013, 17, 1159–1173.
- Ying, K.C.; Liao, C.J. An ant colony system for permutation flow-shop sequencing. Comput. Oper. Res. 2004, 31, 791–801.
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991; Volume 142, pp. 134–142.
- Colorni, A.; Dorigo, M.; Maniezzo, V. A Genetic Algorithm to Solve the Timetable Problem; Politecnico di Milano: Milan, Italy, 1992.
- Hayat, I.; Tariq, A.; Shahzad, W.; Masud, M.; Ahmed, S.; Ali, M.U.; Zafar, A. Hybridization of Particle Swarm Optimization with Variable Neighborhood Search and simulated annealing for Improved Handling of the Permutation Flow-Shop Scheduling Problem. Systems 2023, 11, 221.
- Chen, S.H.; Chang, P.C.; Cheng, T.; Zhang, Q. A self-guided genetic algorithm for permutation flowshop scheduling problems. Comput. Oper. Res. 2012, 39, 1450–1457.
- Baraglia, R.; Hidalgo, J.I.; Perego, R. A hybrid heuristic for the traveling salesman problem. IEEE Trans. Evol. Comput. 2001, 5, 613–622.
- Harik, G.R.; Lobo, F.G.; Goldberg, D.E. The compact genetic algorithm. IEEE Trans. Evol. Comput. 1999, 3, 287–297.
- Mühlenbein, H.; Paaß, G. From recombination of genes to the estimation of distributions I. Binary parameters. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 1996; pp. 178–187.
- Pelikan, M.; Goldberg, D.E.; Lobo, F.G. A survey of optimization by building and using probabilistic models. Comput. Optim. Appl. 2002, 21, 5–20.
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359.
- Tasgetiren, M.F.; Pan, Q.K.; Suganthan, P.N.; Liang, Y.C. A discrete differential evolution algorithm for the no-wait flowshop scheduling problem with total flowtime criterion. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Scheduling, Honolulu, HI, USA, 1–5 April 2007; pp. 251–258.
- Pan, Q.K.; Tasgetiren, M.F.; Liang, Y.C. A discrete differential evolution algorithm for the permutation flowshop scheduling problem. Comput. Ind. Eng. 2008, 55, 795–816.
- Zobolas, G.; Tarantilis, C.D.; Ioannou, G. Minimizing makespan in permutation flow-shop scheduling problems using a hybrid metaheuristic algorithm. Comput. Oper. Res. 2009, 36, 1249–1267.
- Mehrabian, A.R.; Lucas, C. A novel numerical optimization algorithm inspired from weed colonization. Ecol. Inform. 2006, 1, 355–366.
- Zhou, Y.; Chen, H.; Zhou, G. Invasive weed optimization algorithm for optimization no-idle flow shop scheduling problem. Neurocomputing 2014, 137, 285–292.
- Wei, H.; Li, S.; Jiang, H.; Hu, J.; Hu, J. Hybrid genetic simulated annealing algorithm for improved flow shop scheduling with makespan criterion. Appl. Sci. 2018, 8, 2621.
- Tseng, L.Y.; Lin, Y.T. A hybrid genetic algorithm for no-wait flowshop scheduling problem. Int. J. Prod. Econ. 2010, 128, 144–152.
- Qu, C.; Fu, Y.; Yi, Z.; Tan, J. Solutions to no-wait flow-shop scheduling problem using the flower pollination algorithm based on the hormone modulation mechanism. Complexity 2018, 2018, 1973604.
- Agárdi, A.; Nehéz, K.; Hornyák, O.; Kóczy, L.T. A Hybrid Discrete Bacterial Memetic Algorithm with Simulated Annealing for Optimization of the flow-shop scheduling problem. Symmetry 2021, 13, 1131.
- Alawad, N.A.; Abed-alguni, B.H. Discrete Jaya with refraction learning and three mutation methods for the permutation flow-shop scheduling problem. J. Supercomput. 2022, 78, 3517–3538.
- Gao, K.; Yang, F.; Zhou, M.; Pan, Q.; Suganthan, P.N. Flexible job-shop rescheduling for new job insertion by using discrete Jaya algorithm. IEEE Trans. Cybern. 2018, 49, 1944–1955.
- Fathollahi-Fard, A.M.; Woodward, L.; Akhrif, O. Sustainable distributed permutation flow-shop scheduling model based on a triple bottom line concept. J. Ind. Inf. Integr. 2021, 24, 100233.
- Baroud, M.M.; Eghtesad, A.; Mahdi, M.A.A.; Nouri, M.B.B.; Khordehbinan, M.W.W.; Lee, S. A New Method for Solving the flow-shop scheduling problem on Symmetric Networks Using a Hybrid Nature-Inspired Algorithm. Symmetry 2023, 15, 1409.
- Liang, Z.; Zhong, P.; Liu, M.; Zhang, C.; Zhang, Z. A computational efficient optimization of flow shop scheduling problems. Sci. Rep. 2022, 12, 845.
- Alireza, A.; Javid, G.N.; Hamed, N. Flexible flow shop scheduling with forward and reverse flow under uncertainty using the red deer algorithm. J. Ind. Eng. Manag. Stud. 2023, 10, 16–33.
More
