Deep Learning in Hyperspectral Imagery

Deep Learning in Hyperspectral Imagery: Comparison

Please note this is a comparison between Version 1 by Saad Bin Ahmed and Version 2 by Camila Xu.

Deep learning algorithms used for hyperspectral image analysis and processing include artificial neural networks (ANNs), convolutional neural networks (CNNs), Auto-encoder decoders (AEDs), and stacked auto-encoders (SAE). Hyperspectral imagery (HSI) is used because of its characteristic of containing both spectral and spatial information at the pixel level.

hyperspectral imagery
HSI document analysis
spectral unmixing

1. Introduction

Recent advancements in hyperspectral imagery (HSI) image analysis due to its depth coordinates have increased the importance of hyperspectral data to manifolds. However, due to the large dimensionality of the input data, restricted availability, and high intra-class variability, HSI image analysis deep learning (DL) architectures show complexity ^[1][67].

The following are the characteristics that deep learning architecture must exhibit ^[1][67].

With or without manually constructed feature extraction methods, deep learning networks may extract linear and non-linear characteristics from raw data.
Deep learning architectures can handle various forms of data; for example, in the case of HSI datasets, they can handle spectral and spatial data separately and simultaneously as well.
Depending upon the nature of the problem and the type of available dataset, the choice for the architecture and implementation of the learning strategy varies.
Due to the presence of various processing techniques such as batch partition ^[2][68], high-performance computing (HPC) ^[3][69], and parallel computing ^[4][5][70,71], deep learning architectures can better scale when dealing with large amounts of data.

Deep learning architectures’ effectiveness is dependent on the automatic and hierarchical learning process from the spatial domains of the data, as well as the spectral domains in the case of HSI datasets. Given that the deep learning model contains a high number of parameters, a relatively large dataset is required for training so that the overfitting of the learning model can be avoided. A dataset in such a case comprises hundreds of thousands of samples ^[6][72]. As discussed previously, features extracted from HSI data are of the dimensions

X \in ℜ^{n_{1}, n_{2}, n_{b} a n d s}

and are composed of their two spatial components,

n_{1}

and

n_{2}

, and their spectral domain

n_{b a n d s}

. Although these features can be processed through ML models, DNNs stand out by adapting to the processing of such types of features through deep neural net architectures ^[1][67]; however, while implementing DNNs for HSI data the following challenges need to be handled.

Due to their propensity to overfit if the training set only contains a few training samples, DNNs are inefficient at generalizing the distribution of HSI data. The DNN architecture being implemented is more prone to overfitting, necessitating changes during the training phase, limited generalization, and poor performance on the test set in the case of HSI datasets because of the high dimension and sparse training examples.
Due to the curse of dimensionality, DNN architectures for HSI are computationally expensive and memory-intensive.
Deeper networks with more parameters make training, optimization, and convergence more challenging and could result in several local minima.
With the training process being a black box and the number of parameters for HSI, although various visualization processes can be implemented to visualize output at every layer, implementing optimization decisions and implementing more significant and interpretable filters is a tedious job.

Due to the above-mentioned challenges and issues, researchers and developers have attempted to implement DNNs as shown in Figure 16, choosing the best-fit learning strategies and optimization processes that are best suited for HSI datasets while maintaining computational efficiency ^[1][67].

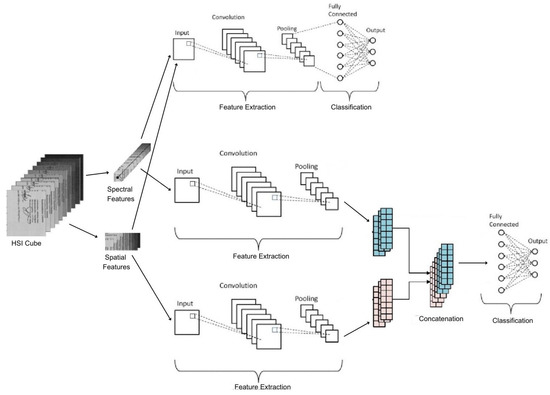
Figure 16.

Deep Learning Pipeline for HSI Data.

A major portion of work implemented through HSI datasets is related to the remote sensing field, with all methods and functions being dedicated to the remote sensing or geo-spatial field specifically, with very little work being implemented in other domains such as forensics, document analysis, biomedical, target detection, anomaly detection, data enhancement, etc. ^[6][72].

2. HSI Data Handling

In the case of HSI datasets, most available datasets comprise few hundred samples with relatively higher dimensionality, which may or may not be labeled, leading to the issue of sparsity because of the presence of a lesser number of samples that contribute to training, and the inability of the model to generalize training on such data may lead to overfitting. Such issues may be resolved by implementing unsupervised techniques, which are specialized to learn the network in the absence of labeled data.

By extracting spectral signatures from either individual pixels or groups of pixels, DL architectures focus on HSI data work by extracting the data in a pixel-by-pixel fashion. For instance, an object-detection approach must be constructed before obtaining object-wise spectral signatures. To resolve the curse of dimensionality issue and the redundancy issues that come with dimensionality reduction methods like PCA ^[7][73], independent component analysis (ICA) ^[8][74] and stacked auto-encoders ^[9][75] have been implemented to extract the problem-relevant features instead of handling the large number of dimensions of HSI datasets followed by spatial processing or 3D-patch processing ^[6][72].

The number of layers, kinds of layers (such as convolution, pooling, activation, softmax layers, etc.), activation function, problem to be solved, and learning procedures are the factors that determine how efficient and successful a deep neural network is. The most popular deep learning architectures incorporate characteristics such as space-invariance ^[10][76], robustness, and deformation; require fewer data; and implement powerful regularization techniques ^[11][77].

3. Deep Neural Network (DNN) Architecture

The perceptron is the fundamental building block of every neural network, and it is responsible for performing computation from single-layer to complex deep learning architectures. Neural networks are aggregations of neurons taking inputs in the form of either an input to the whole network from the input layer or an input in the form of the output of the preceding layer. A neuron takes all inputs, aggregates them, and produces the output, which may be passed to another neuron in the proceeding layer, which may be a component of the activation layer, a fully connected layer, a convolution layer, or a pooling layer. The depth of the network, type of activation used, number of pooling layers, and type of layers depend on the nature of the dataset to be processed ^[1][67].

Multiple deep learning architectures have been implemented to handle and process hyperspectral data, some of which are based on the CNN ^[12][78], autoencoder–decoder ^[13][79], generative adversarial neural networks ^[14][80], or the recurrent neural networks ^[15][81]. Implementations of a few of these architectures are detailed in Table 14 and explained as follows.

3.1. CNN Architectures for HSI Data

CNNs have become an important component in hyperspectral image analysis. Hyperspectral imaging is a powerful technology that creates a three-dimensional data cube including both spatial and spectral information by acquiring several images at different wavelengths across the electromagnetic spectrum. However, the analysis of hyperspectral images poses difficulties due to the substantial volume of data present in the multiple channels of the HSI cube formed.

The utilization of CNNs is well suited for hyperspectral image analysis due to their capacity to autonomously acquire spatial attributes and accomplish the precise classification of hyperspectral data. Through the utilization of convolutional layers, CNNs can extract spatial features from the hyperspectral image, with pooling layers aiding in reducing the dimensionality of these extracted features. This process empowers the network to effectively learn the spatial characteristics and achieve accurate classification results for the hyperspectral data.

CNNs have been used to perform a variety of hyperspectral image-processing tasks, such as segmentation, detection, and classification. For example, CNNs have been used for land-cover classification, where they can accurately classify different land-cover types based on their spectral signatures ^[16][17][82,83]. CNNs have also been used for target detection, where they can detect targets such as mines or vehicles in a hyperspectral image ^[18][19][84,85]. CNNs have also been utilized for hyperspectral image segmentation, which divides the image into various sections according to its spectral and spatial characteristics.

Given the high dimensionality of HSI images, methods that work by utilizing both spatial and spectral data into a single-CNN architecture lead to better results as compared to the architectures that utilize either spatial or spectral dimensions. Such techniques have been implemented for HSI and Lidar datasets, thus utilizing the full potential of HSI and LiDAR data and providing improved results ^{[20][21][22][23]}[86,87,88,89]. Different techniques combine spatial and spectral information in a single configuration using feature extraction from many sources at different levels and are used by single or multi-stream CNNs to achieve robust feature extraction. Various approaches involve two-channel CNNs where a 2D CNN focuses on spatial features and 1D CNN focuses on spectral features that are then cascaded at different levels through a cascade network. Similarly, a two-stream CNN with each stream processing data of a different type from a different source and then fusing them in the final convolution layer has also been implemented for land-cover classification through HSI images ^[6][72].

Table 14.

Deep Learning Methods for HSI Images.

Architecture Details	Nature of Dataset	Studies
Convolutional Neural Network (CNN)
Sixty-three images of the City of San Francisco from a custom dataset that was gathered using Google Earth	Satellite Images	Chen et al. ^[16][82]
Sixty-three images of the City of San Francisco from a custom dataset that was gathered using Google Earth	Satellite Images	Chen et al. ^[17][83]
Custom dataset of 25 hyperspectral images of the porcine eye cornea	Porcine eye cornea images	Noor et al. ^[18][84]
Indian Pines & Salinas Valley Dataset	Satellite Images	Yang et al. ^[19][85]
Houston & Trento Dataset	Satellite Images	Rasti et al. ^[20][86]
Houston & Trento Dataset	Satellite Images	Li et al. ^[21][87]
Houston Dataset	Satellite Images	Feng et al. ^[22][88]
ICVL & CAVE Dataset	Street Scene Images	Chang et al. ^[24][90]
Kennedy Space Center, Indian Pines, Pavia University, Salinas Scene datasets are used to evaluate the proposed DL architecture	Satellite & Urban Images	Luo et al. ^[25][91]
Kennedy Space Center, Indian Pines, Pavia University, Salinas Scene datasets are used to evaluate the proposed DL architecture	Satellite & Urban Images	Chen et al. ^[26][92]
Custom Diseased Leaves Dataset	Diseased Leaves Images	Liu et al. ^[27][93]
Indian Pines, University of Pavia, WHU-Hi-HongHu dataset	Satellite Images	Dong et al. ^[28][94]
Autoencoder-Decoder (AED) Architecture
Kennedy Space Center & University of Pavia Datasets	Satellite & Urban Images	Lin et al. ^[29][95]
Indian Pines, Pavia University, Salinas Scene datasets are used to evaluate the proposed DL architecture	Satellite & Urban Images	Shi et al. ^[30][96]
Indian Pines & KSC datasets	Satellite & Urban Images	Zhao et al. ^[31][97]
Indian Pines, Pavia University & Salinas Scene dataset	Satellite & Urban Images	Dou et al. ^[32][98]
Pavia University, Indian Pines, Salinas Scenes dataset	Satellite & Urban images	Zhou et al. ^[9][75]
Indian Pines, Salinas Scenes, Houston datasets	Satellite & Urban Images	Patel et al. ^[33][99]
Generative Adversarial Networks (GANs)
Indian Pines & Pavia University datasets	Satellite & Urban Images	Zhong et al. ^[34][100]
Salinas Valley, Pavia University, KSC dataset	Satellite & Urban Images	Zhu et al. ^[35][101]
Houston, Indian Pines, Xuzhou Dataset	Satellite Images	He et al. ^[36][102]
Indian Pines, Houston2013, Houston2018 dataset	Satellite & Urban Images	Hang et al. ^[37][103]
Recurrent Neural Networks (RNNs)
Indian Pines, Pavia University, Salinas Scenes dataset	Satellite & Urban Images	Zhang et al. ^[38][104]
Indian Pines & Pavia University dataset	Satellite Images	Hang et al. ^[39][105]
Houston, Indian Pines & Pavia University dataset	Satellite & Urban Images	Mou et al. ^[40][106]
Indian Pines, Pavia center scene & Pavia University dataset	Satellite & Urban Images	Shi et al. ^[41][107]
Indian Pines, Big Indian Pines & Salinas Valley dataset	Satellite & Urban Images	Paoletti et al. ^[42][108]

Chang et al. implemented a deep denoising CNN for HSI image restoration in which the learned filters extract spatial information and the spectral data are learned and extracted through the multiple channels of the 2-D filters without distorting the features of the original HSI image and removing different distributions of noise ^[24][90].

A CNN-based architecture was proposed by Luo et al. to extract spatial–spectral properties from the target pixel and its surrounding pixels. The extracted features are then transformed into one-dimensional feature maps using convolutions, which are stacked into a 2D matrix to serve as the input image for a standard CNN. The researchers implemented two variations of this network, one incorporating XGBoost and the other utilizing the MNIST model. They conducted performance evaluations on benchmarked hyperspectral image (HSI) datasets, including Kennedy Space Center (KSC), Indian Pines (IP), Pavia University, and Salinas Scenes. The results showed improved accuracy compared to existing CNN architectures commonly used as benchmarks ^[25][91].

In order to enhance the performance of HSI classification, Chen et al. implemented 1D Auto-CNNs and 3D Auto-CNNs as spectral-spatial classifiers. They also chose the appropriate number of operations for convolution, pooling, identity, batch normalization, activation function selection, architecture selection, and regularization techniques. The model is then evaluated on the Kennedy Space Center (KSC) dataset, the Indian Pines (IP), Pavia University dataset, and the Salinas Scenes datasets, resulting in better outcomes compared to cutting-edge deep CNN models ^[26][92].

Lu et al. have implemented a 3D atrous denoising CNN architecture for HSI images that extracts feature maps both spatially and spectrally, and the proposed multi-branch architecture leads to less training issues, less overfitting risk and texture preservation, leading to the removal of photon and thermal noise. The proposed architecture’s results are superior to those of modern denoising architectures ^[27][93].

To improve the categorization of hyperspectral images (HSIs), Dong et al. have put out a brand-new method dubbed Weighted Feature Fusion of Convolutional Neural Network and Graph Attention Network. To increase accuracy, they make use of the capabilities of graph neural networks (GNN) and graph attention networks (GATs). A graph attention network (GAT) is first put into practice using an encoder–decoder design. It then includes an attention mechanism in a convolutional neural network (CNN). The features that were extracted from both networks are then fused together after being given weights. The suggested approach outperforms current state-of-the-art models in the area of HSI classification, according to thorough testing and evaluation ^[28][94].

In conclusion, CNNs are an effective tool for hyperspectral image processing and may be applied to a variety of tasks, such as segmentation, detection, and classification.

3.2. Autoencoder–Decoder Architectures for HSI Data

An autoencoder is a neural network used for unsupervised learning, comprising an encoder and a decoder. This network architecture collaboratively learns a condensed representation of the input data. The encoder reduces the dimensions of the input data, while the decoder uses this compressed representation to recreate the original data.

In the domain of hyperspectral image analysis, autoencoders offer a valuable technique for acquiring a hyperspectral image representation in low dimensions. The process involves the encoder component taking a high-dimensional hyperspectral image as input and creating an image’s compressed version in a smaller-dimensional space. Subsequently, the decoder component reconstructs the original image using this compressed representation.

The autoencoder undergoes training using a collection of hyperspectral images, attempting to keep the difference between the original image and the reconstruction as small as possible. Following the training phase, the autoencoder becomes capable of compressing novel hyperspectral images into a condensed representation of lower dimensionality. This compressed representation finds utility in diverse applications, including image classification, anomaly detection, and target detection.

Due to their inherent high dimensionality and redundant information, autoencoders are used in hyperspectral image analysis. The rationale behind using autoencoders is to acquire a condensed, hyperspectral image represented in reduced dimensions. This enables a reduction in computational complexity during subsequent analysis tasks while still retaining the vital information within the data.

Lin et al. discussed a framework for spectral–spatial feature extraction through the autoencoder–decoder (AED) architecture. They implemented PCA on the spectral dimension and autoencoder-decoder (AED) architecture in the spatial dimension to extract features for classification. Representations are computed via autoencoders and then passed on to the classifier, and for spatial dimensions, PCA is implemented while keeping the first three principal components. The representations from the AED and the principal components from PCA are further passed through the training AED layers and a final logistic regression layer ^[29][95].

Shi et al. have developed a classification framework for hyperspectral image (HSI) analysis that leverages the concept of spectral–spatial features extracted from multi-scale super-pixels using recurrent neural networks (RNN) and stacked autoencoders. The approach involves segmenting the HSI image into shape-adaptive regions using multi-scale super-pixels, which capture object information with enhanced accuracy. By incorporating the super-pixel-based method, the algorithm effectively captures features at various scales and utilizes the RNN architecture to account for feature correlations across different scales ^[30][96].

Zhao et al. have introduced a methodology that involves measuring hyperspectral images (HSI) of suitable spatial resolution using pixel-based transformations and class separability criteria. The next step is a hierarchical learning architecture that combines a random forest classifier and a deep-stacked sparse autoencoder. This method’s goal is to use high-level, abstract feature representations that include both spatial and spectral data. The architecture achieves a favorable balance between generalization, prediction accuracy, and operational speed. The researchers conducted experiments on the Indian Pines and Kennedy Space Center datasets, resulting in competitive, state-of-the-art outcomes ^[31][97].

Dou et al. developed a band-selection technique for hyperspectral image (HSI) datasets, aiming to reduce redundancy while preserving the original content of the dataset. The HSI data samples are recreated using a small number of useful bands for each pixel in their method, which considers band selection as a challenge of spectral reconstruction. The non-linear inter-dependencies between bands are modeled using an attention-based autoencoder. The autoencoder uses the most informative bands found for each pixel using the attention module to rebuild the raw HSI. By grouping the column vectors of the obtained attention mask and choosing the most representative band for each cluster, the final band selection is accomplished. This approach enables the learning of global non-linear correlations among the bands. The suggested algorithm uses the stochastic gradient descent algorithm to jointly optimize all parameters. The architecture is evaluated on HSI datasets such as Indian Pines, Pavia University, and Salinas, yielding promising and encouraging results ^[32][98].

Zhou et al. have tackled the challenge of achieving both low intra-class scatter and large inter-class separation to effectively learn a low-dimensional feature space for hyperspectral image (HSI) classification. They propose a novel architecture called the compact and discriminative stacked autoencoder (CDSAE), consisting of two stages that progressively optimize the feature mappings. In the first stage, Fischer Discriminant Regularization is applied to the hidden layers of the stacked autoencoder. This regularization encourages the network to map pixels belonging to the same class closer together while minimizing reconstruction errors during training. The feature representations obtained from this stage, which include the Fischer discriminant regularization, are then used by the classifier. To prevent the network from becoming excessively deep, the authors employ diverse regularization techniques on the hidden neurons. The University of Pavia, Indian Pines, and Salinas datasets are used to assess the proposed model’s performance in HSI categorization ^[9][75].

Patel et al. have proposed an autoencoder based on the CNN architecture for HSI classification, keeping in consideration the huge volume of hyperspectral picture data and limited spatial resolution. By utilizing autoencoders in the initial layers, hyperspectral feature augmentation allows for the acquisition of optimized weights in the initial layers. Therefore, using this approach, features are extracted from the pre-processed HSI data and employed by the classifier via a shallow CNN architecture. The method has since been evaluated on the Indian Pines, Pavia University, Salinas Scene, and Houston datasets, with encouraging results showing that it is comparable with state-of-the-art methods ^[33][99].

3.3. Generative Adversarial Neural Networks (GANs) for HSI Data

Generative Adversarial Networks (GANs) are a specific class of deep neural network architectures that prove highly advantageous in generating new data samples closely resembling an existing dataset. In the field of hyperspectral image analysis, GANs offer the potential to generate novel hyperspectral images that exhibit similarities to the original dataset. This capability can be harnessed for diverse purposes such as data augmentation, denoising, and other relevant applications.

GANs operate on the principle of training two deep neural networks concurrently: a generator network and a discriminator network. The discriminator network takes a sample as input and distinguishes between actual and generated/fake samples, whereas the generator network takes a random noise vector as input and generates a new sample. During training, the generator network gains the ability to produce samples that closely resemble genuine samples, making it harder for the discriminator network to tell them apart. Simultaneously, the discriminator network learns to distinguish between genuine and artificial data with accuracy.

In the context of hyperspectral image analysis, the generator network within GANs can be trained to generate novel hyperspectral images that exhibit similarity to the original dataset. Conversely, it is possible to train the discriminator network to distinguish between actual hyperspectral images and those produced by the generator. Once the GAN is trained, the generator network becomes capable of producing new hyperspectral images, which can be utilized for various purposes, including data augmentation or other relevant applications.

Some of the challenges of using GANs in hyperspectral image analysis are as follows.

Data dimensionality: Hyperspectral data typically have high-dimensional feature spaces, which can make training GANs more complex and computationally demanding. The increased dimensionality can lead to difficulties in capturing the intricate distributions and correlations present in hyperspectral data.
Limited training data: GANs often require a large number of training data to effectively learn and generate high-quality samples. However, collecting and labeling large-scale hyperspectral datasets can be expensive and time-consuming, resulting in limited training data availability for GAN models.
Mode collapse: Mode collapse refers to a situation where the generator network fails to capture the full diversity of the target hyperspectral data distribution and instead produces only a limited set of samples. This can result in generated hyperspectral images that lack variability and fail to represent the entire data distribution.
Evaluation and validation: Assessing the quality and performance of GAN-generated hyperspectral data can be challenging. Metrics and evaluation methods specific to hyperspectral data need to be developed to ensure the generated samples are accurate representations of the original data and satisfy domain-specific requirements.
Sensitivity to noise and artifacts: GANs can be sensitive to noise and artifacts present in hyperspectral data. This noise and artifacts can affect the training process and influence the quality of the generated samples, requiring additional preprocessing steps or regularization techniques to mitigate their impact.

Addressing these challenges and developing robust GAN architectures tailored for hyperspectral data analysis can lead to improved generation and utilization of synthetic hyperspectral data for various applications.

To address the classification of hyperspectral images (HSIs), Zhong et al. have suggested a system that combines a generative adversarial network (GAN) with a conditional random field (CRF). This approach combines a probabilistic graph model and semi-supervised deep learning. By employing convolutions and transposed convolutions, the authors extract discriminative features from labeled HSI samples. These features are then used as input to GANs, which generate additional labeled HSI samples. This approach addresses the issue of limited labeled training data. Dense CRFs are constructed using random variables initialized with the softmax predictions from the GANs. The CRFs are further fine-tuned on the HSI data to obtain refined classification maps ^[34][100].

Zhu et al. implemented a CNN and a GAN for fake image classification. They implemented a 1D GAN for spectral classification and a 3D GAN for spectral–spatial classification. The CNN and GANs are trained concurrently, and the GAN distinguishes between the fake data and the genuine data by creating false inputs from the original data. Training both together fine-tunes the discriminative CNN, increases the generalization capability of the discriminative CNN, and also solves the issue of fewer original training samples. The proposed pipeline is tested on Salinas, Indian Pines, and Kennedy Space Center dataset ^[35][101].

He et al. have tackled the challenge of class imbalance in GANs, where the minority class is often associated with a fake label. To overcome this issue, they have introduced a semi-supervised GAN that incorporates a transformer architecture. This transformer is semi-supervised to prevent self-contradiction during classification and discrimination tasks. The generator, equipped with skip connections, is responsible for generating HSI patches, while, to prevent the loss of critical information during the generating process, the transformer captures the semantic context. The generalization capability of the transformer is enhanced through data-augmentation techniques. On the Houston, Indian Pines, and Xuzhou datasets, the suggested model is assessed, and it exhibits competitive classification performance when compared to leading-edge models ^[36][102].

By using the vast quantity of information included in unlabelled HSI data, Hang et al. suggested a multitask generative adversarial network (MTGAN) to cope with the issue of the poor availability of HSI training examples. The generator network reconstructs the HSI cube, including the labeled and unlabelled areas, and then attempts to recognize the class of the cube through its classification module. The cube coming from the reconstructed data and the original data is distinguished using a discriminator network, whose generalizability is improved as it receives the original input samples and the nearly original reconstructed samples from the generator. Skip connections are implemented in the generator, and the classifier module to make use of information in the shallow layers. The outcomes of the suggested architecture are compared to those of the state of the art in ^[37][103].

3.4. Recurrent Neural Networks (RNN) for HSI Data

RNNs, a specific type of neural network, are suitable for handling sequential data processing tasks. When applied in hyperspectral image analysis, RNNs prove beneficial in processing the sequential information embedded within hyperspectral images.

Hyperspectral images capture the spectral response of each pixel across numerous wavelengths, forming a sequence of spectral bands. RNNs can efficiently handle these sequences by extracting useful features that may be used in a variety of hyperspectral image analysis applications, such as classification. Using an RNN known as a Long Short-Term Memory (LSTM) network is one such strategy. The vanishing gradient issue that might arise when using standard RNNs to process lengthy data sequences is addressed by LSTMs. Within hyperspectral image analysis, the application of LSTM networks involves handling input sequences consisting of spectral bands. Each band represents the spectral response of a pixel at a specific wavelength. The LSTM network processes this sequential data, enabling the extraction of features that encapsulate both spatial and spectral attributes present in the image. Then, these characteristics may be applied to categorization or other tasks suc as target or anomaly detection. A prominent area of study in the domain of remote sensing is the application of RNNs in hyperspectral image processing, which has demonstrated promising results.

In order to analyze hyperspectral pixels as sequential data and fill in any missing categories, Mou et al. have introduced a neural network architecture based on RNNs. In contrast to conventional rectified linear units or tanh, the authors’ method uses the parametric rectified tanh (PRetanh) activation function, which permits the use of larger learning rates without worrying about divergence during training. To enhance the efficiency of processing hyperspectral data and reduce parameter complexity, a modified gated unit is employed in the recurrent layer. Three aerial hyperspectral image datasets are used to assess the proposed model, producing results that are competitive in terms of performance ^[40][106].

To use redundant and supplementary information seen in hyperspectral images (HSIs), Hang et al. devised a cascaded RNN architecture using gated recurrent units. The suggested model has two layers, the first of which seeks to remove duplicate information between neighboring spectral bands and the second of which aims to collect supplementary information from non-adjacent HSI bands. An integrated convolutional module with convolutional layers handles the spectral–spatial properties of the HSI data. Two HSI datasets are used to test the model’s performance, and the results are not as competitive as those from other current models ^[39][105].

Zhang et al. have devised an RNN-based approach, known as the local spatial sequential (LSS) method, to effectively extract both local and semantic information from hyperspectral images. In order to create LSS features, the approach first extracts low-level data such as texture and morphological profiles. The RNN architecture is then given these LSS characteristics for additional processing. The RNN generates high-level features, which are then passed through a softmax layer for final classification. To further enhance performance, the researchers introduce a non-local spatial sequential method into the RNN architecture, referred to as NLSS-RNN. This method identifies non-local similar structures and incorporates their information into the LSS features, preserving spatial information and integrating knowledge from non-local similar samples. The suggested method is tested on several HSI datasets and produces competitive results that exceed cutting-edge techniques ^[38][104].

In order to explicitly address the issue of high dimensionality in HSI data, Paoletti et al. have developed an enhanced RNN architecture for hyperspectral image (HSI) classification. Recognizing that conventional RNNs struggle to handle large datasets and high-dimensional input, the researchers designed a modified RNN with simpler recurrent units. This enhanced architecture not only offers competitive classification accuracy but also demonstrates improved scalability when dealing with HSI data ^[42][108].

Recurrent neural networks (RNNs) have been used by Shi et al. to offer a novel framework for hyperspectral image (HSI) classification that captures the spatial dependence and spectral–spatial characteristics of nearby pixels. They suggest multi-scale hierarchical recurrent neural networks (MHRNNs) to circumvent RNNs’ restriction to processing just 1D sequences. They create multi-scale image patches of the focal and peri-focal pixels to carry out this method, and then they use 3D convolutional neural networks (CNNs) to extract local spectral–spatial information. The spatial dependency at various scales is then captured by building multi-scale 1D sequences based on the 3D local spectral–spatial properties and employing MHRNNs. In order to produce competitive visual results and classification accuracy, the suggested architecture takes into account both local spectral–spatial properties and the spatial dependence of non-adjacent picture patches. Performance evaluation demonstrates its state-of-the-art performance ^[41][107].