Your browser does not fully support modern features. Please upgrade for a smoother experience.
Please note this is a comparison between Version 2 by Rita Xu and Version 1 by Akira Kawamura.
Since the 20th century, Japan has experienced a period of very rapid urbanization. Cities have experienced substantial densification and expansion, resulting in gradually elevated flood risk. Urban flooding has also occurred in most large cities in Japan, particularly in Tokyo. In response to this growing problem, much effort and resources have been spent on research and development aimed at understanding, simulating, and managing urban flood risk in Japan.
- urban flood risk assessment
- USF model
- urban landscape GIS delineation
1. Introduction
Development in urban areas greatly increases surface runoff, owing to the increase in impervious surfaces, as well as the total runoff volume flowing to the receiving watershed. In addition, the construction of storm sewer systems and the culverting of rivers during the urbanization process increase the runoff rate. The peak velocity of runoff inevitably increases as more runoff is discharged at shorter intervals, resulting in an increased risk of overflow. In conjunction with the concentration of population and property in the watershed, urbanization thus generally makes flood potential higher [1,2,3,4][1][2][3][4].
Since the latter half of the 20th century, urbanization has progressed rapidly in both developed and developing countries. Especially in Japan, urbanization has progressed much more rapidly than in Europe and the United States [5]. Mountains and hills in watershed areas that had been forests and fields were developed one after another, and agricultural land, including paddy fields, was simultaneously converted into residential land [5]. As a result, the watersheds were transformed into urban areas with a high risk of inundation. In an urban watershed, there is a complex distribution of artificially developed impervious areas, such as houses, buildings, paved roads, and parking lots, where rainwater cannot infiltrate. Runoff pathways by storm drainage facilities, such as sewers and artificial drainage channels, as well as runoff control and flood control facilities (e.g., storage and infiltration facilities), form a very complex urban runoff system that is constantly changing [6]. In Japan, the 1958 Kano River Typhoon Event is considered the first case of urban flooding [7], which caused extensive inundation damage not only in the lowlands but also in previously flood-free plateau areas [7,8][7][8].
In terms of flood damage in Japan, there has been a decreasing trend in human losses, although the economic losses have not decreased. The damage per unit area has exhibited an upward trend since the 2000s. Recent floods in urban areas have become more complex than past urban floods. One reason is the increasing frequency of unpredictable localized torrential rains, commonly called “guerrilla downpours” [9,10[9][10][11],11], which might be considered to be an effect of urbanization [12]. Seino et al. [13] explored how urbanization affects precipitation in the Tokyo metropolitan area. The risk of pluvial flooding caused by surcharge from sewerage facilities has been shown to increase compared to fluvial flooding caused by overflow from river channels [14].
Urban flooding, especially associated with recent record-breaking rainfall events, has become one of the most pressing social issues. Thus, flood mitigation is a crucial water management strategy for reducing destructive damage. For this purpose, rainfall-runoff models are important tools that play a central role, especially in urban watersheds. Generally, the purpose of runoff analysis is to clarify the physical mechanism of the runoff process by applying the amount of precipitation (rainfall, snowfall, etc.) to predict hydrological impacts, such as floods and droughts, in the target watershed. The results are used for the planning and management of rivers and watersheds.
In terms of process description, runoff models can be classified into two main types: lumped and distributed models. The former considers the watershed as a homogeneous unit without spatial variability, and the runoff process is generally expressed as ordinary differential equations of time. Distributed models explicitly consider the spatial variability of watershed characteristics and are usually expressed as partial differential equations of time and place [15,16][15][16]. In addition, semi-distributed models also exist, where a watershed is divided into sub-watersheds, each of which is represented by a lumped model. Based on how the response of runoff as output to rainfall (precipitation) as input is described, models may be classified into “response models”, which simply use a response relationship, “conceptual models”, which conceptualize the response relationship, and “physical models”, which model the runoff from the basic equations of physics.
The most commonly used lumped conceptual models in Japan today are the tank model [17] and the storage function (SF) model [18,19][18][19]. The tank model was developed by Sugawara in 1956 [17], and the SF model was proposed by Kimura in 1961 [18,20][18][20]. The SF model is a lumped model used to simulate individual flood events and has the ability to represent nonlinearity in the runoff process with a relatively simple structural equation and fast calculation. The SF model is commonly used in watersheds with relatively large catchment areas under the jurisdiction of the Ministry of Land, Infrastructure, and Transport (MLIT), and has become the standard runoff model for flood control planning in Japan [21,22,23,24][21][22][23][24].
In contrast to lumped models, distributed models explicitly incorporate the spatial variability of watershed characteristics. With the widespread use of Geographic Information System (GIS) technology, distributed physical models have been widely used in small-to-medium-sized urban watersheds, where the effects of land use change and flood control facility development on runoff characteristics have been evaluated [25,26,27][25][26][27]. The main advantages of commonly used grid-based distributed models are their simple structure and their use of spatially explicit watershed information, which is generally readily available. Because of these advantages, grid-based distributed models are widely used not only in rural areas but also in urban watersheds. In Japan, Sayama et al. [28] proposed the rainfall-runoff-inundation (RRI) model, which is a 2D model capable of simultaneously analyzing rainfall runoff and flood inundation. The RRI model has been integrated with modeling and visualization tools by the International Centre for Water Hazard and Risk Management (ICHARM) of the Public Works Research Institute (PWRI) [29] and is used not only in Japan but also in other countries.
Globally, many different basin-scale hydrological models have been developed, including the TOPMODEL [30], Xinanjiang model [31[31][32],32], Systeme Hydrologique Europeen (SHE) [33], and the Institute of Hydrology Distributed model (IHDM) [34], and those are also commonly used in Japan. The Hydrologiska Byrån Vattenbalans (HBV) model was developed in Sweden in the 1970s and has been widely used worldwide [35]. More recently, the hydrological processes for the environment (HYPE) model [36,37][36][37] was developed, which has been set up from the basin to the global scale and is used for operational forecasting as well as climate change impact assessment. Tanouchi et al. [21] developed the semi-distributed HYPE model to improve the description of urban runoff.
The accurate characterization of impervious surface type and extent is required for the prediction of the corresponding impacts on watershed hydrology [38]. However, in general, the land use information used as watershed characteristics in grid-based models is simply the impervious area ratio and the runoff coefficient. Therefore, the ability to accurately represent the impermeable characteristics of urban watersheds in grid-based models is limited [39]. Many models use raster-type land use data generated from aerial photographs.
With recent technological advances in GIS, digital information has become readily available for urban watersheds. In addition to grid-shaped raster land use information, vector-type polygonal (polygon shape) land use data, which can accurately represent buildings, roads, and other land features, have also been created [40]. However, there are still only a few cases in which polygon-type land use information is directly used for runoff analysis. Sample et al. [41] used GIS to facilitate urban stormwater analysis using land use parcel boundaries. Rodriguez et al. [42] used a vector-based watershed description based on a so-called urban databank, which includes the categories cadastral parcel, building, street, sewer system, and river, to calculate an urban unit hydrograph. Lee et al. [43] developed a model to evaluate low-impact development (LID) by defining a watershed as a hydrological response unit (HRE), which is a sub-watershed for calculating stormwater inflow to the sewer system. However, the area of the HRE is very big at several thousand square meters, and land use information is averaged over the HRE.
2. Brief History on Urban Runoff Modeling in Japan
In Japan, Morita [48][44] characterized an urban watershed as a so-called “small- to medium-sized urban river basin”, where most of the watershed is flat land, such as alluvial plains, flood plains, alluvial fans, and hills. Normally, the entire upper, middle, and lower reaches are developed into urban areas, and the watershed area is generally smaller than 100 km2. As for urban runoff research in Japan, Kinoshita [1] was the first to comprehensively and quantitatively describe and discuss urban flood runoff mechanisms in 1967. This preseaperrch was followed by numerous studies on urban flood runoff mechanisms [2,3][2][3], which were summarized by Kadoya [4] in 1985. There, the urban flood runoff mechanisms are characterized by (1) an increased runoff rate during floods, (2) a reduced flood concentration time before rainwater flows into rivers, and (3) extremely large peak runoff rates due to high-intensity rainfall peaks with a short duration. Generally, most of the flood runoff models were mainly intended for mountainous and natural watersheds and were not developed with urban watersheds in mind, as pointed out in the Hydrology and Water Resources Handbook published by JSHWR in 1997 [49][45]. In addition, physical runoff processes in urban watersheds are not fundamentally different from those in natural watersheds. As a result, when applying a runoff model to an urban watershed, only the model parameters are usually adjusted [49][45]. The rational equation [50][46], which is used in many small-to-medium-sized river and sewage system plans in Japan, was originally proposed as a model for estimating peak flows as a basis for stormwater management in urban watersheds. Parameters, such as the runoff coefficient and flood concentration time, need to be calibrated for the target urban watershed. For example, in 1976, Kadoya and Fukushima [51][47] proposed an equation relating flood concentration time to flood magnitude based on the equivalent roughness method. The synthesized rational formula [52,53][48][49] has also been developed as a model for urban watersheds in 1998. This method creates a hydrograph by dividing an urban watershed into sub-watersheds, each characterized by area, runoff coefficient, and flood concentration time, and combining the peak flows by superimposing the results from the rational equation. The quasi-linear storage model [54][50] developed in 1977 and the modified RRL method [55][51] developed in 1972 are also used as flood runoff models for urban areas by setting flood concentration times and runoff coefficients for the urban watershed of interest [56,57][52][53]. In 1954, Iwagaki and Sueishi applied the kinematic wave theory to the analysis of hillslope runoff [58,59][54][55], and soon after, Lighthill and Whitham [60][56] developed the kinematic wave theory for river flow tracking. Since then, this theory has been accepted as a standard tool for modeling surface flows and various other elementary hydrological processes [61,62][57][58]. The kinematic wave model, in which the watershed is described in terms of a collection of rectangular slopes and river channels, and rainwater flow, which is represented by a hydraulic continuity equation and a kinematic equation, is a widely used distributed physical model in Japan (see, for example, [24,62][24][58]). As an example of applications of the kinematic wave model to urban watersheds, in 1991, Ando et al. [63][59] divided an urban watershed into rectangular sub-watersheds using spatially distributed rainfall and applied the kinematic wave model to each divided sub-watershed. The reproducibility of the hydrograph was improved by using the equivalent roughness value of the urban watershed as an input. In 1995, Fujimura et al. [64][60] showed that diffusion wave or dynamic wave models are more accurate than kinematic wave models for nonstationary and unsteady river channel flow calculations, although kinematic wave models are used for the slope flow, as well as surface flow, of low-lying watersheds. In 1996, Suzuki et al. [65][61] developed the Doken model as a distributed model for real-time flood forecasting. The model has been incorporated into the Integrated Flood Analysis System (IFAS) for flood forecasting in watersheds with inadequate water level observations and has been applied in Asian countries, such as Pakistan [66][62]. In 1997, Chikamori et al. [67][63] attempted to obtain model parameters, such as equivalent roughness, using GIS information when constructing a kinematic wave model for an urban watershed. In the Technical Standard for River Erosion Control, Survey Edition by MILT [68][64], the rational equation [50][46], the SF model [18], the kinematic wave model [24], the quasi-linear storage model [54][50], the tank model [17], and the Doken model [65][61] are introduced as runoff models. Since then, along with the rapid development of computer and IT technology, the analysis of flood runoff in urban watersheds has been improved in several respects. Data collection by, e.g., satellites and radar is a significant advancement, as is the advancement of GIS technology [69][65]. Furthermore, a range of new methods based on, e.g., optimization methods, network theory, and AI, have been applied to flood runoff analysis and modeling. Shibuo and Furumai [70][66] recently reviewed urban stormwater management in Japan, focusing on rainfall observations, numerical modeling, and emerging technologies.3. Rainfall and Water Level Observation System in Japan
A key component of flood runoff modeling is access to observational data. In Japan, information on rainfall and river levels is mainly provided by the Water Information and National Land Data Management Centre established by the Water Management and Land Conservation Bureau under the MLIT [71][67]. As of 2023, real-time river observations (water level and streamflow) and rainfall observations are provided online at 7580 and 10,619 stations, respectively [72][68]. In particular, the recently developed crisis water level gauges have improved river level monitoring during heavy rainfall, with approximately 6000 stations installed from 2018 to 2020. For rainfall, in addition to these, approximately 1300 precipitation monitoring stations have been installed by the Japan Meteorological Agency (JMA) through the Automated Meteorological Data Acquisition System (AMeDAS), with one station per 17 km2 across the country [73][69]. The X-band multi-parameter (MP) network of weather radars, known as the eXtended RAdar Information Network (XRAIN), was developed in 2008 by MLIT. The network uses 16 high-performance C-band MP radars and 39 X-band MP radars that are specialized for rainfall observation [74][70]. XRAIN provides high-resolution (250 m), high-frequency (1 min), and near-real-time rainfall information for almost the entire land area of Japan without the need for correction by rain gauges at the ground surface. However, owing to its short wavelength, XRAIN has only a narrow observation area (80 km radius) because of attenuation caused by rainfall, and in some cases, it cannot fully penetrate heavy rainfall areas. In urban areas, small-to-medium-sized rivers are at high risk of river overflow and flood damage due to flooding caused by short periods of high-intensity rainfall. Therefore, urban runoff analysis requires very high-resolution observations to accurately capture the spatial and temporal distributions of rainfall. Schilling [75][71] suggested that rainfall data of at least 1–5 min and 1 km resolutions should be used for urban drainage modeling. Fabry et.al. [76][72] recommended the use of higher-resolution data (1–5 min temporal and 100–500 m spatial) for urban hydrological applications to provide the necessary hydraulic details. In the case of localized torrential rainfall, there is often a delay of only tens of minutes from the start of the rainfall to the peak river water level, and flooding damage associated with such events is frequent in large cities in Japan [77][73]. For this reason, the validation of flood runoff analysis models for urban areas requires a time resolution of river observations similar to that of the rainfall observations. In Tokyo, for example, the Tokyo Metropolitan Flood Control Integrated Information System (FCIS) plays a role in flood prevention activities by automatically collecting real-time observations of rainfall and river water levels in Tokyo and providing them to the relevant organizations [78][74]. The FCIS began observing 10 min rainfall in January 1978 and later increased the resolution to 1 min. Water level observations were initiated to inform residents of the danger of flooding due to the rapid increase in water levels caused by heavy rainfall. A total of 124 water level observation stations were established in Tokyo, and 15 stations (1.67 km2/station) were established in the Kanda River basin. Rainfall observations were introduced to measure high-intensity rainfall with high resolution in time and space, as well as high precision. The number of rainfall observation stations has increased annually, and as of 2022, 93 stations (19 km2/station) have been installed (Figure 1). This is a very large number, considering that there are only 10 AMeDAS stations operated by the JMA [73][69] in Tokyo (178 km2/station). FCIS data are expected to accurately describe the spatial variability of heavy rainfall.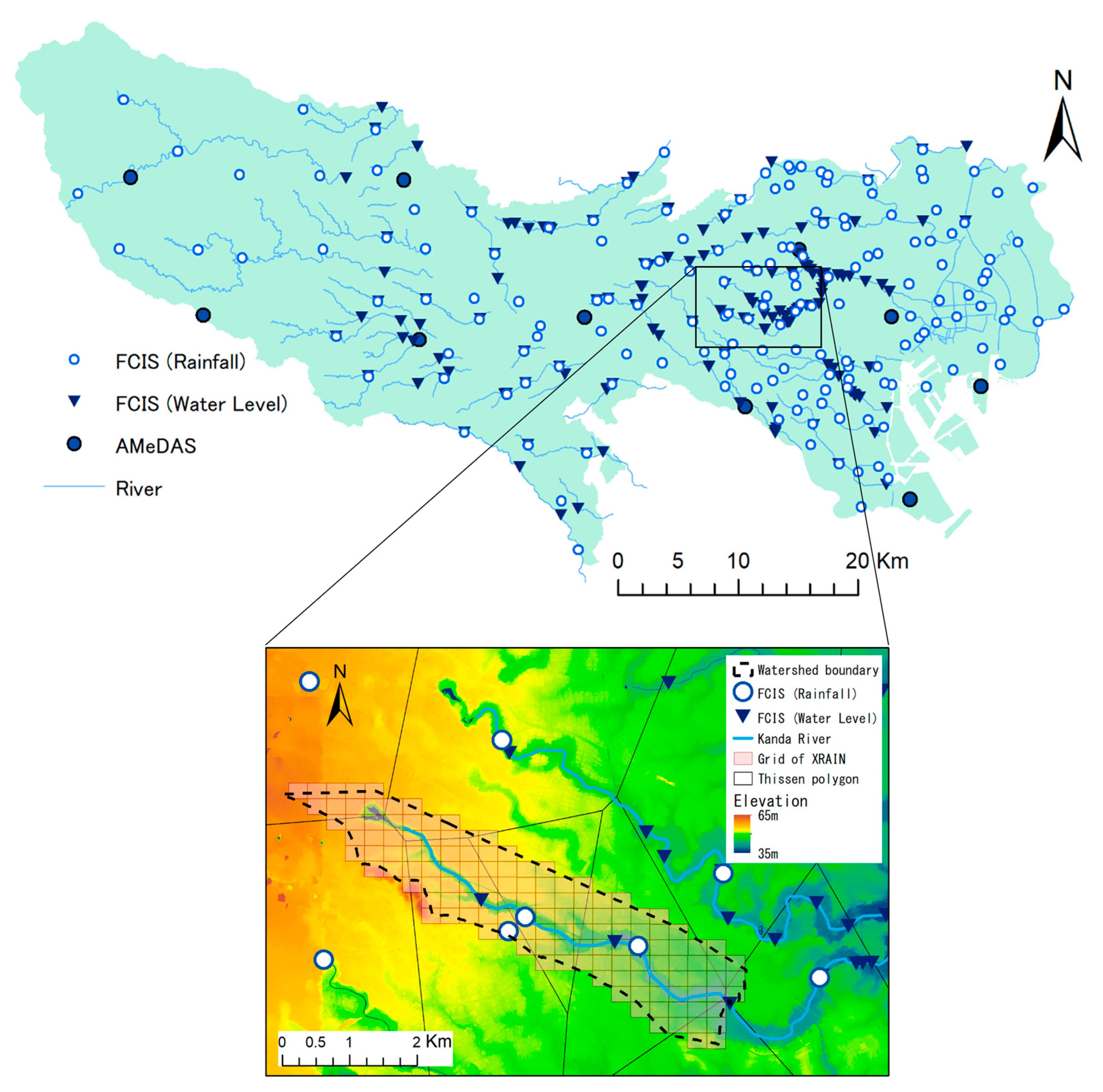
Figure 1. Map of FCIS and AMeDAS stations in Tokyo Metropolis (top) and a zoomed-in map of FCIS stations and XRAIN grid in the upper Kanda River Watershed (bottom).
References
- Kinoshita, T. Runoff changes due to urbanization. Civ. Eng. Technol. Mat. 1976, 9, 11–15. (In Japanese)
- Takahashi, Y.; Izumi, K.; Ando, Y.; Kanao, K. Change of flood runoff in hilly basins by urbanization. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1982, 26, 261–266. (In Japanese)
- Yamada, T.; Ishii, F.; Yamazaki, K.; Iwatani, K. On relation between distribution of field moisture capacity and runoff characteristics in small basins. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1985, 29, 25–30. (In Japanese)
- Kadoya, M. A review of the study on runoff changes due to urbanization. J. Jpn. Soc. Civ. Eng. 1985, 363, 23–34. (In Japanese)
- Takahashi, Y. City and Water; Iwanami Shinsho: Tokyo, Japan, 1988; pp. 1–34. (In Japanese)
- Amaguchi, H.; Kawamura, A.; Olsson, J.; Takasaki, T. Development and testing of a distributed urban storm runoff event model with a vector-based catchment. J. Hydrol. 2012, 420–421, 205–215.
- Tamai, N. River Engineering; Ohmsha: Tokyo, Japan, 1999; pp. 55–95. (In Japanese)
- Ishihara, S.; Takasaki, T.; Kawamura, A.; Amaguchi, H. Background of new development plan and future development methods of urban rivers in Tokyo metropolis. Adv. River Eng. 2014, 20, 437–442. (In Japanese)
- Kanae, S. Characteristics of localized torrential rainfall (so-called guerrilla rainfall). J. Hydrol. Syst. 2009, 73, 11–16. (In Japanese)
- Nakakita, E.; Yamaguchi, K.; Yamabe, H. A study on detecting origin of localized torrential rainfall using volume scanning radar. DPRI Annu. 2008, 52, 547–562. (In Japanese)
- Ushiyama, M. A study of relationship between “Guerilla Heavy Rainfall” and disaster. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2011, 67, I_505–I_510. (In Japanese)
- Fujibe, F.; Togawa, H.; Sakata, M. Long-term change and spatial anomaly of warm season afternoon precipitation in Tokyo. SOLA 2009, 5, 17–20.
- Seino, N.; Aoyagi, T.; Tsuguti, H. Numerical Simulation of Urban Impact on Precipitation in Tokyo: How does Urban Temperature Rise Affect Precipitation? Urban Clim. 2018, 23, 8–35.
- Kawamura, A. Urban flooding and its countermeasures. In Urban Technology, Revised ed.; Graduate School of Urban Infrastructure and Environment, Tokyo Metropolitan University, Ed.; Gihodo Pub.: Tokyo, Japan, 2016; pp. 235–249. (In Japanese)
- Singh, V.P. Watershed modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 1–22.
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary; JSCE: Tokyo, Japan, 1999; pp. 35–47. (In Japanese)
- Sugawara, M. Rainfall-Runoff Analysis; Kyoritsu Pub: Tokyo, Japan, 1972; p. 257. (In Japanese)
- Kimura, T. Storage Function Model. Civ. Eng. J. 1961, 3, 36–43. (In Japanese)
- Kawamura, A. Inverse problems in hydrology. In Introduction to Inverse Problems in Civil Engineering; Jpn. Soc. Civil Eng.; Maruzen: Tokyo, Japan, 2000; pp. 24–30. (In Japanese)
- Hino, M. What have hydrologists done and what should we do? What should we do from now on? J. Jpn. Soc. Hydrol. Water Res. 1996, 9, 3–16. (In Japanese)
- Tanouchi, H.; Olsson, J.; Lindstrom, G.; Kawamura, A.; Amaguchi, H. Improving urban runoff contributions in multi-basin hydrological simulation by the HYPE model using EEA Urban Atlas. Hydrology 2019, 6, 28.
- Baba, H.; Hoshi, K.; Hashimoto, N. Synthetic storage routing model coped with loss mechanisms. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1999, 43, 1085–1090. (In Japanese)
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Araki, K. Storage function model considering urban runoff process. J. Jpn. Soc. Civ. Eng. B 2009, 65, 217–230. (In Japanese)
- Shiiba, M.; Tachikawa, Y.; Ichikawa, Y. Hydrology and Hydraulic Engineering Planning Studies; Kyoto University Press: Kyoto, Japan, 2013; pp. 351–371. (in Japanese)
- Hanaki, T.; Suharyanto, A.; Sugio, S. Investigation of flood control by rainwater infiltration facilities in urbanized watershed. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1999, 48, 37–42. (In Japanese)
- Jia, Y.; Ni, G.; Kinouchi, T.; Yoshitani, J.; Kawahara, Y.; Suetsugi, T. Study on effects of storm-water detention facilities in an urbanized watershed using distributed model. Jpn. Soc. Civ. Eng. Hydraul. Conf. 2001, 45, 109–114. (In Japanese)
- Amaguchi, H.; Kawamura, A. A proposal of urban runoff model considering green infrastructures and its application. J. Jpn. Soc. Civ. Eng. Ser. G (Environ. Res.) 2020, 76, I_319–I_325. (In Japanese)
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall-runoff-inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312.
- Public Works Research Institute. RRI Model. Available online: http://www.icharm.pwri.go.jp/research/rri/rri_top.html (accessed on 18 November 2022).
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69.
- Zhoa, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381.
- Ren, L.; Yuan, F. The Xinanjiang model on a digital basin platform. In Watershed Models; Singh, V.P., Frevert., D.K., Eds.; CRC Press: Boca Raton, FL, USA, 2006; pp. 179–208.
- Bathurst, J.C.; Wicks, J.M.; O’Connell, P.E. The SHE/SHESED basin scale water flow and sediment transport modelling system. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 563–594.
- Calver, A.; Wood, W.L. The Institute of Hydrology Distributed Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 595–626.
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 443–476.
- Lindström, G.; Pers, C.P.; Rosberg, R.; Strömqvist, J.; Arheimer, B. Development and test of the HYPE (Hydrological Predictions for the Environment) model—A water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319.
- SMHI, HYPE. Available online: https://www.smhi.se/en/research/research-departments/hydrology/hype-1.7994 (accessed on 18 November 2022).
- Koga, T.; Kawamura, A.; Amaguchi, H. Study on permeable area ratio of 10m-mesh land use classification using advanced GIS delineation in the upper Kanda River basin. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, I_505–I_510. (In Japanese)
- Amaguchi, H.; Kawamura, A.; Takasaki, T. Physically based distributed flood runoff model for an urban catchment using polygon feature GIS data. J. Jpn. Soc. Civ. Eng. B 2007, 63, 206–223. (In Japanese)
- Koga, T.; Kawamura, A.; Amaguchi, H.; Tanouchi, H. Assessing impervious area ratios of grid-based land-use classifications on an example of an urban watershed. Hydrol. Sci. J. 2016, 61, 1728–1739.
- Sample, D.J.; Heaney, J.P.; Wright, L.; Koustas, R. Geographic information systems, decision support systems, and urban storm-water management. J. Water Plan. Man. 2001, 127, 155–161.
- Rodriguez, F.; Andrieu, H.; Creutin, J.D. Surface runoff in urban catchments: Morphological identification of unit hydrographs from urban databanks. J. Hydrol. 2003, 283, 146–168.
- Lee, J.G.; Nietch, C.T.; Panguluri, S. Drainage area characterization for evaluating green infrastructure using the storm water management model. Hydrol. Earth Syst. Sci. 2018, 22, 2615–2635.
- Morita, S. Urban Flood Risk Analysis; Forum 8: Tokyo, Japan, 2014; pp. 3–75. (In Japanese)
- Matsubayashi, U. Runoff mechanism and characteristics in urban areas. In Handbook of Hydrology and Water Resources; Jpn Soc. Hydrol. Water Res.; Asakura: Tokyo, Japan, 1997; pp. 146–148. (In Japanese)
- Ishikawa, K.; Sato, K.; Izumi, K. Applicability of rational method to the urbanized channels in Tokyo. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1982, 26, 267–272. (In Japanese)
- Kadoya, M.; Fukushima, A. Concentration time of flood in small or medium river basin. DPRI Annu. 1976, 19B, 143–152. (In Japanese)
- Tanioka, Y.; Fukuoka, S.; Taniguchi, M.; Koyama, Y. Characteristics of floods in small urban rivers. J. Jpn. Soc. Civ. Eng. 1998, 586, 1–12. (In Japanese)
- Watanabe, A.; Sasada, T.; Watanabe, N.; Yamada, T. Theoretical derivation of synthesized rational formula. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 74, I_973–I_978. (In Japanese)
- Hashimoto, T.; Hasegawa, T. A runoff model to evaluate land use change. Civ. Eng. J. 1977, 19, 221–226. (In Japanese)
- Yamaguchi, T.; Matsubara, S.; Yamamori, T. Second report of rainfall-runoff study in an urban area -Runoff estimation by modified R.R.L. method. Civ. Eng. J. 1972, 14, 34–39. (In Japanese)
- Matsubayashi, U. Runoff model for urban watersheds. In Handbook of Hydrology and Water Resources; Jpn. Soc. Hydrol. Water Res.; Asakura: Tokyo, Japan, 1997; pp. 148–151. (In Japanese)
- Sukegawa, N.; Kitagawa, Y. A rainfall-runoff simulation model for assessing the effect of urbanization on flood runoff. Proc. Jan. Soc. Civ. Eng. 1982, 325, 51–59. (In Japanese)
- Iwagaki, Y.; Sueishi, T. On the unsteady flow in open channels with uniform lateral inflow—Hydraulic studies on the run-off phenomena of rain water, 1st report. J. Jpn. Soc. Civ. Eng. 1954, 39, 575–583. (In Japanese)
- Sueishi, T. On the run-off analysis by the method of characteristics hydraulic studies on the run-off phenomena of rain water, 2nd report. J. Jpn. Soc. Civ. Eng. 1955, 29, 74–87. (In Japanese)
- Lighthill, M.J.; Whitham, G.B. On kinematic waves: 1. Flood movement in long rivers. Proc. R. Soc. 1955, 229, 281–316.
- Singh, V.P.; Jain, S.K. Rainfall-Runoff Modeling. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill Education: New York, NY, USA, 2016; Chapter 59; pp. 59-1–59-8.
- Kimura, M.; Tanaka, T.; Azechi, I.; Nakatani, K.; Yamazaki, D.; Yoshioka, H. Interdisciplinary perspective of surface water flow numerical analysis. J. Jpn. Soc. Hydrol. Water Res. 2017, 30, 307–334. (In Japanese)
- Ando, Y.; Nabeyama, T.; Nishijima, S. Flood runoff analysis of urban watersheds. J. Urban Res. 1991, 41, 69–89. (In Japanese)
- Fujimura, K.; Ando, Y.; Maeda, M. A study on stormwater runoff model of urban lowland basin. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1995, 39, 61–66. (In Japanese)
- Suzuki, T.; Terakawa, Y.; Matsuura, T. Development of physics-based distributed model for operational hydrological forecasting. Civ. Eng. J. 1996, 38, 26–31. (In Japanese)
- Shahzad, A.; Gabriel, H.F.; Haider, S.; Mubeen, A.; Siddiqui, M.J. Development of a flood forecasting system using IFAS: A case study of scarcely gauged Jhelum and Chenab river basins. Arab. J. Geosci. 2018, 11, 383.
- Chikamori, H.; Oka, T.; Takara, K.; Okubo, G. Fundamental Study on Application of Geographic Information System to Construction of Rainfall-Runoff Model of Urbanized Area. DPRI Annu. 1997, B 40, 137–144. (In Japanese)
- Ministry of Land, Infrastructure, Transport and Tourism. Investigation Guidelines for River Sand and Gravel Management Technology Standards, Survey Edition; MLIT: Tokyo, Japan, 2016; Chapter 3.
- Kawamura, A. Status quo and perspectives of flood runoff analysis for urban watersheds. J. Jpn. Soc. Hydrol. Water Res. 2018, 31, 451–466. (In Japanese)
- Shibuo, Y.; Furumai, H. Advances in Urban Stormwater Management in Japan: A Review. J. Disaster Res. 2021, 16, 310–320.
- Water Management and Land Conservation Bureau. Available online: https://www5.river.go.jp/ (accessed on 27 March 2023).
- Water Management and Land Conservation Bureau. River Disaster Prevention Information. Available online: https://city.river.go.jp/kawabou/reference/index01.html (accessed on 27 March 2023).
- Japan Meteorological Agency. Automated Meteorological Data Acquisition System 2020. Available online: https://www.jma.go.jp/jma/en/Activities/amedas/amedas.html (accessed on 10 November 2022).
- Ministry of Land, Infrastructure, Transport and Tourism. X-Band MP Radar Network. Available online: http://mp-radar.bosai.go.jp/mlit.htm (accessed on 18 November 2022).
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21.
- Fabry, F.; Bellon, A.; Duncan, M.R.; Austin, G.L. High resolution rainfall measurements by radar for very small basins: The sampling problem reexamined. J. Hydrol. 1994, 161, 415–428.
- Koyama, N.; Sakai, M.; Yamada, T. Study on a Water-Level-Forecast Method Based on a Time Series Analysis of Urban River Basins—A Case Study of Shibuya River Basin in Tokyo. Water 2023, 15, 161.
- Tokyo Metropolitan Government—Flood Control Integrated Information System. Available online: https://www.kasen-suibo.metro.tokyo.lg.jp/im/uryosuii/tsim0102g_en.html (accessed on 10 November 2022).
More
