We consider the time reversal T and particle-antiparticle C symmetries that, being most fundamental, can be violated at microscopic level by a weak interaction. The notable example here is from condensed matter, where strongly correlated Fermi systems like HF metals and high-Tc superconductors (or HF compounds) exhibit C and T symmetries violation due to the so-called non-Fermi liquid (NFL) behavior rather than to microscopic inter-particle interaction. When a HF compound is near the topological fermion condensation quantum phase transition (FCQPT), it exhibits the NFL properties, so that the C symmetry breaks down, making the differential tunneling conductivity to be an asymmetric function of the bias voltage V. This asymmetry does not take place in normal metals, where Landau Fermi liquid (LFL) theory holds. Under the application of magnetic field, a HF compound transits to the LFL state, and σ(V) becomes symmetric function of V. These findings are in good agreement with experimental observations. We suggest that the same topological FCQPT defines the baryon asymmetry in the Universe. Thus, the most fundamental features of the nature are defined by its topological and symmetry properties.
- quantum phase transition
- fermion condensation
- tunneling conductivity
- time-reversal symmetry
- baryon asymmetry
- strongly correlated Fermi systems
1. Introduction
It is well-known that ordinary electric conductivity in a metal does not depend on the sign of bias voltage V. This is because it does not depend on the charge (positive or negative) of a particle (in a solid this corresponds to so-called quasiparticle) which carries the electric current. To be specific, in ordinary metals both electron or hole conductivities are similar to each other, making the resulting conductivity ϭ(V) to be a symmetric function. On the other hand, if the symmetry due to charge conjugation (so-called
C
-symmetry or
C
-parity) is violated, the ϭ(V) function becomes asymmetric: ϭ(V) ≠ ϭ(-V). The violation of
C
(as well as time reversal
T
and parity
P) symmetry is usually related to some of the most fundamental features of a physical system: under normal conditions these symmetries are kept intact, signifying that nothing happens. This means that asymmetry of conductivity in a solid signifies some fundamental rearrangement of its physical properties. It is well-known that the discovery of the CP violation in elementary particle physics resulted in Nobel prize. Fundamental symmetries are a powerful method to gain information about physical system spanning from atoms in solids to the galaxies and their clusters in the Universe. Knowledge of such symmetries and conditions for their violation permit us to ascertain general knowledge about physical systems without solving any equations, latter often very complicated. Quite frequently, the microscopic approach to condensed matter (e.g., computer simulations) gives only particular information about specific solids (or class of solids with identical symmetries of their crystal lattice, but still with different microscopic interatomic interactions) but not about universal features, inherent in wider class of physical systems.
) symmetry is usually related to some of the most fundamental features of a physical system: under normal conditions these symmetries are kept intact, signifying that nothing happens. This means that asymmetry of conductivity in a solid signifies some fundamental rearrangement of its physical properties. It is well-known that the discovery of the CP violation in elementary particle physics resulted in Nobel prize. Fundamental symmetries are a powerful method to gain information about physical system spanning from atoms in solids to the galaxies and their clusters in the Universe. Knowledge of such symmetries and conditions for their violation permit us to ascertain general knowledge about physical systems without solving any equations, latter often very complicated. Quite frequently, the microscopic approach to condensed matter (e.g., computer simulations) gives only particular information about specific solids (or class of solids with identical symmetries of their crystal lattice, but still with different microscopic interatomic interactions) but not about universal features, inherent in wider class of physical systems.
Among above so-called discrete symmetries (which oppose so-called continuous symmetry like symmetries of time – dependent characteristics of motion), the charge conjugation one is particularly intriguing. The main problem here is the fundamental question of inequality between matter and anti-matter in the universe. The point is that normally the C-symmetry of the physical laws suggests that there should be equal amounts of both in the universe. At the same time, this is not true as now we have high excess of the matter over antimatter. This topic is still hotly debated in the literature. This means that the differential conductivity can probe the fulfillment of the fundamental laws of Nature.
One of the peculiar situations, taking place in metallic solids, is the so-called topological fermion condensation quantum phase transition (FCQPT)
One of the peculiar situations, taking place in metallic solids, is the so-called topological fermion condensation quantum phase transition (FCQPT)
https://en.wikipedia.org/wiki/Quantum_phase_transition
, when the topology of corresponding Fermi surface is altered, see e.g.
[1]
. As a result of this transition, some of the fermions, comprising strongly correlated Fermi system, condense like bosons, see Refs
[2]
,
[3]
,
[4]
for details. These condensed fermions form the fermion condensate (FC), which is responsible for many salient features, observed in the above systems. Among other things, the corresponding theoretical approach describes well the non-Fermi liquid (NFL) behavior demonstrated by the strongly correlated Fermi systems
[5]
,
[6]
. The same approach, being applied to the differential tunneling conductivity of strongly correlated fermionic solids like heavy-fermion (HF) metals demonstrates that latter quantity becomes significantly asymmetric function of bias voltage V. The underlying physical mechanism is the same as that in the archetypical HF metal YbRh
2
Si
2
, where external parameters place the electronic subsystem near FCQPT point in the phase diagram. The aforementioned asymmetry has been observed experimentally in HF metals (compounds) both in normal and superconducting state, see, e.g.
[5]
.
2. Asymmetry in HF Metals
To illustrate the strength of the FC-based approach, we consider the temperature dependence of the asymmetric part of point contact spectra on YBa
2
Cu
3
O
7−x
/La
0.7
Ca0.3MnO3 bilayers with Tc = 30 K. The data showing that asymmetric part of the conductivity ϭ
asym
(V) remains constant up to Tc and persists up to temperatures well above

Figure 1 [3]. Temperature dependence of the asymmetric part ϭ
Temperature dependence of the asymmetric part ϭ
asym
(V) extracted from measurements on YBa2Cu3O7−x/La0.7Ca0.3MnO3 bilayers of the differential conductivity at different temperatures
[7]
. The dashed line shows the linear dependence of ϭ
asym
(V) on the variable V over a wide range.
Tc. It is seen that ϭ
asym
(V) starts to diminish at T>Tc. These observations are in excellent agreement with theory and are strong evidence, supporting the FC theory. In order to find out if the electron density is nonuniform in Bi2Sr2CaCu2O8+x, the spectroscopic measurements have been undertaken, see Ref.
[8]
. These measurements were augmented by tunneling microscopy at low temperatures. The manifestation of the above non-uniformity is local DOS and superconducting gap spatial fluctuations. The inhomogeneity observed in the integrated DOS is not induced by impurities but is the inherent property of the system. This is supported by observations relating the value of the integrated local DOS to the concentration x of local oxygen impurities. Spatial variations in the differential tunneling conductivity spectrum are shown in Figure 2. Clearly, the differential tunneling conductivity of Bi2Sr2CaCu2O8+x is highly asymmetric in its superconducting state. Figure 2 shows the asymmetric conductivity obtained from
[8]
. Indeed, for small values of V, ϭ
asym
(V) is a linear function of voltage and the slopes of the respective straight lines are inversely proportional to the size of the superconducting gap. At sufficiently low temperatures and under the application of magnetic field B, the standard behavior, described by the Landau theory of Fermi liquid is restored, along with the
C
and
T
symmetries. As a result, the asymmetric part of the tunneling conductivity vanishes. To observe the finite asymmetry of the conductivity, the measurements must be carried out when HF metals under consideration demonstrate the NFL behavior characterized by the particle-hole asymmetry. Latter asymmetry is the typical feature of HF metals located near the topological FCQPT. Thus, we conclude that the emergence of ϭ
asym
(V) is the typical NFL feature. The differential resistance as a function of the current I can also be a hallmark of the NFL properties and the violation of
C
and
T
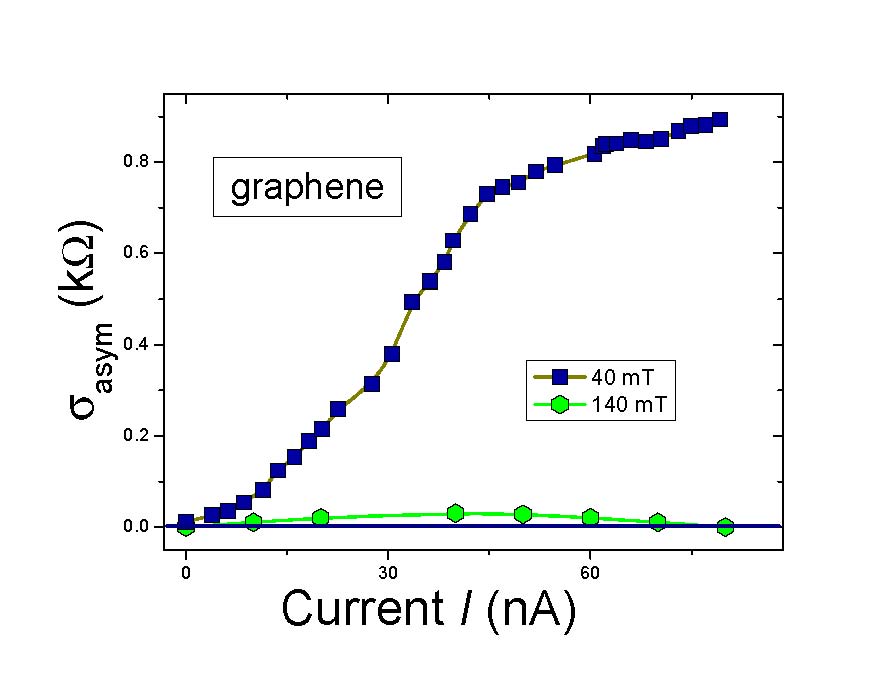
symmetries. For instance, the differential resistance has been measured in graphene
[9]
. It had been shown experimentally that the asymmetric part of the differential resistance diminishes as the magnetic field increases. This observation is of great importance since graphene has a perfect flat band generated by the topological FCQPT that violates the particle-hole symmetry
[3]
,
[9]
. Notably, it has been suggested that the band flattening leads to the time-reversal symmetry breaking
.
Figure 2. The asymmetric part of the differential resistance ϭ
asym
(kΩ)=dV/dI(I)−dV/dI(−I) is extracted from experimental data, obtained in measurements on graphene
[9]
. It is clearly seen that under the application of tiny magnetic field the asymmetry vanish
[3]
.
3. Violation of T and C Symmetries in the Universe
The interconnection of different fields of physics is comprised by the complicated and fundamental relations among its different branches, for instance between solid state physics and astrophysics. Latter relations, being of core importance, give an example of the fundamental relation between the very large and very small. As discussed in the Introduction, the demonstrated above, violation of the charge conjugation symmetry
C
in solids has its large-scale counterpart in the asymmetry between matter and antimatter in the early Universe. This is because the weak interaction does not alter the baryon number conservation, that guarantees the stability of a proton
[11]
. In this case, the FCQPT concept delivers the underlying physical mechanism for both aforementioned processes. This implies that the FC phenomenon spans from the atomic scale to that of the Universe and hence is rather general and not an accidental in nature. Since the details of matter-antimatter (baryon) asymmetry are discussed in details
[3]
, here we make some general remarks regarding this question. It is well-known (see, e.g.,
[11]
) that the relation between particles and antiparticles in the Universe is governed by so-called combined
CP
symmetry, which is the result of successive action of charge conjugation (
C
), transforming a particle into antiparticle (electron into hole and vice versa in solids) and parity (
P
), which reverses the directions of spatial coordinates. The time inversion symmetry,
T
, changes t to -t. The overall symmetry thus transforms particles into antiparticles. The common wisdom is that during and shortly after the Big Bang, the number of particles in the Universe was approximately equal to that of antiparticles. Later on, as the temperature fell, this equality vanished, giving rise to the current, highly asymmetric state.
Note that in solids electrons and holes are so-called quasiparticles (roughly speaking, quantized elementary excitations of some ground state or vacuum); in cosmology the particles (antiparticles) correspond to baryons (antibaryons), which are the real elementary particles with a nonzero rest mass, made from quarks and antiquarks
[12]
. The mapping of “very small” (quasiparticles in solids) onto “very large” (baryons in the Universe) can be best understood using a spontaneous symmetry-breaking concept. Like in solids, where the symmetries is often broken in different phase transitions (for instance in quantum phase transitions as temperature is reduced to zero or almost zero), it is believed that the Universe, during cooling down, went through a series of symmetry-breaking quantum phase transitions. One of them is the above discussed FCQPT. Under the supposition that a hole in a Fermi liquid is a baryon, while the quasiparticle is an antibaryon, we can easily see the correspondence between particle-hole (in a solid) and baryon-antibaryon (in the Universe) symmetries. In this case, to describe the observed asymmetric conductivity theoretically, one should inevitably use the FC approach
. We note that although fundamental microscopic interaction in the FC formalism is invariant with respect to quasiparticles and holes interchange, it yields spontaneous
C
and
T
symmetries breaking at low temperatures due to the topological reconstruction of the Fermi surface. This reconstruction yields the dependence of the quasiparticle spectrum in FC phase on different external stimuli, which, in turn, generates NFL anomalies in observable properties of HF metals and high-Tc superconductors. This quantum phase transition, in turn, breaks the particle-hole symmetry, generating, inter alia, the observable asymmetric conductivity. Similar argumentation can be utilized to gain insights into baryon-antibaryon asymmetry in the Universe. Note that it fits perfectly into the existing cosmological models. The baryon-antibaryon asymmetry has been explained in
[3]
in terms of macroscopic FCQPT which looks almost similar to that in HF metals but in much larger scale. In the parameter space, the Universe gets to the FCQPT point after the initial inflation during the strong (by 10 orders of magnitude) cooling. As the result of FCQPT, the fermion condensate appeared in the Universe. Latter condensate is indeed a source of excess of matter over the antimatter. At further cooling, the Universe acquired the NFL properties, generated by the above fermion condensate. Our analysis shows, that latter condensate may generate the breakdown of
C
and
T
symmetries, thus distorting the particle-antiparticle balance in the Universe and the time arrow emerges. At finite temperatures baryon-antibaryon asymmetry reenters as an inherent property of the system located in the FC state. Latter property is due to the topological transformation of the Fermi sphere accompanied by deviation of the distribution function from the step function at low temperatures. As the temperature decreases, the system approaches the FC state with the corresponding flat band which increases the asymmetry violation. The details rely upon the specific form of interparticle interaction. This mapping of the quasiparticles in solids to the baryons gives some hint to the origin of symmetries in the Universe as salient features of condensed matter can readily be verified experimentally as well as computed numerically and sometimes analytically. The correspondence between micro (condensed matter) and macro (cosmology) physics should be further studied. This is because while in condensed matter, almost every property is accessible experimentally, in cosmology we cannot judge about its underlying physics directly. Rather, in this case, indirect methods should be used. One of such indirect methods is the correspondence between the stellar objects and their condensed matter counterparts. As the properties of the ground state (corresponding to a vacuum in the Universe that can be represented by both the dark energy and the dark matter) in solids are well understood both from ab initio calculations and experiment, the above correspondence allows to shed light on such topics of cosmology and particle physics as the existence of the time arrow, the large entropy and the absence of the antimatter in the Universe.
Here we discuss two phenomena which are seemingly very far away from each other: the asymmetric conductivity in solids with strongly correlated fermions and baryon asymmetry in the Universe. We have already shown that the asymmetric part of the tunneling conductivity/resistivity in solids arises due to the fermion condensation phenomenon in the corresponding substance. This shows that the low-temperature properties of strongly correlated fermion systems are universal, and this universality allows us to consider some classes of strongly correlated systems, namely HF compounds, as representing the new state of matter in the sense that this state do not depend on either atomic properties of HF compounds or, for a large scale case, on the microscopic details of baryons in the Universe. The universality, in turn, is due to the fact, that the considered fermion condensation phenomenon occurs due to the change of the topological class of the corresponding Fermi surface. This immediately implies the universality of both the above asymmetries, based on a topology, is one more milestone of the contemporary physics—the topological class of an object can reveal a lot about its physical properties
Here we discuss two phenomena which are seemingly very far away from each other: the asymmetric conductivity in solids with strongly correlated fermions and baryon asymmetry in the Universe. We have already shown that the asymmetric part of the tunneling conductivity/resistivity in solids arises due to the fermion condensation phenomenon in the corresponding substance. This shows that the low-temperature properties of strongly correlated fermion systems are universal, and this universality allows us to consider some classes of strongly correlated systems, namely HF compounds, as representing the new state of matter in the sense that this state do not depend on either atomic properties of HF compounds or, for a large scale case, on the microscopic details of baryons in the Universe. The universality, in turn, is due to the fact, that the considered fermion condensation phenomenon occurs due to the change of the topological class of the corresponding Fermi surface. This immediately implies the universality of both the above asymmetries, based non a topology, is one more milestone of the contemporary physics—the topological class of an object can reveal a lot about its physical properties
. We argue here, that existing microscopic approaches, based either on model calculations within Hubbard and Kondo models or simulations (constructed actually from more sophisticated versions of the latter models) cannot describe adequately the appearance and destruction of asymmetric conductivity in solids. We speculate that the presented FC theory, which is based on general topological and symmetry arguments, can explain not only the above discussed but many other properties of seemingly different physical objects from an uniform point of view
[6]
. To the best of our knowledge, the effective theories of gravity, even their quantum versions, cannot explain the baryon asymmetry, the existence of time arrow, the large entropy and other yet unexplained problems of contemporary cosmology and large-scale astronomy.
References
- Strongly correlated quantum spin liquid . WiKi. Retrieved 2020-12-3
- V.A. Khodel; V.R. Shaginyan; V.V. Khodel; New approach in the microscopic Fermi systems theory. V.A. Khodel; V.R. Shaginyan; New approach in the microscopic Fermi systems theory. Physics Reports 1994, 249, 1-134, 10.1016/0370-1573(94)00059-x.
- V. R. Shaginyan; A. Z. Msezane; G. S. Japaridze; V. A. Stephanovich; Violation of the Time-Reversal and Particle-Hole Symmetries in Strongly Correlated Fermi Systems: A Review. V.R. Shaginyan; A. Z. Msezane; V.A. Stephanovich; V.A. Stephanovich; Violation of the Time-Reversal and Particle-Hole Symmetries in Strongly Correlated Fermi Systems: A Review. Symmetry 2020, 12, 1596, 10.3390/sym12101596.
- G. E. Volovik; Flat Band and Planckian Metal. JETP Letters 2019, 110, 352-353, 10.1134/s002136401917003x.
- V. R. Shaginyan; M. Ya. Amusia; A. Z. Msezane; K. G. Popov; Scaling behavior of heavy fermion metals. Vasily Shaginyan; M. Ya. Amusia; A. Z. Msezane; K. G. Popov; Scaling behavior of heavy fermion metals. Physics Reports 2010, 492, 31-109, 10.1016/j.physrep.2010.03.001.
- Miron Amusia; Vasily Shaginyan; Strongly Correlated Fermi Systems: A New State of Matter. Springer Tracts in Modern Physics 2020, 283, 385, 10.1007/978-3-030-50359-8.
- S Piano; Fabrizio Bobba; A De Santis; F. Giubileo; A Scarfato; A M Cucolo; Point Contact Spectra on YBa2Cu3O7−x/La0.7Ca0.3MnO3bilayers. Journal of Physics: Conference Series 2006, 43, 1123-1126, 10.1088/1742-6596/43/1/273.
- S. H. Pan; J. P. O'neal; R. L. Badzey; C. Chamon; H. Ding; J. R. Engelbrecht; Z. Wang; H. Eisaki; S. Uchida; A. K. Gupta; et al.K.-W. NgE. W. HudsonK. M. LangJ. C. Davis Microscopic electronic inhomogeneity in the high-Tc superconductor Bi2Sr2CaCu2O8+x. Nature 2001, 413, 282-285, 10.1038/35095012.
- Yuan Cao; Valla Fatemi; Shiang Fang; Kenji Watanabe; Takashi Taniguchi; Efthimios Kaxiras; Pablo Jarillo-Herrero; Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43-50, 10.1038/nature26160.
- V.R. Shaginyan; A. Z. Msezane; V. A. Stephanovich; G. S. Japaridze; E. V. Kirichenko; Flat bands and strongly correlated Fermi systems. Vasily Shaginyan; Alfred Z. Msezane; V. A. Stephanovich; George S Japaridze; Elena Kirichenko; Flat bands and strongly correlated Fermi systems. Physica Scripta 2019, 94, 065801, 10.1088/1402-4896/ab10b4.
- Marco Sozzi; Discrete Symmetries and CP Violation. OxfoMarco Sozzi; Discrete Symmetries and CP Violation. Discrdete University Press Symmetries and CP Violation 2007, 22, 568, 10.1093/acprof:oso/9780199296668.001.0001.
- David Griffiths; Introduction to Elementary Particles. WDavid Griffiths; Introduction to Elementary Particles. ILntroduction to EY‐VCH Verlag GmbH & Co. KGaA lementary Particles 1987, 56, 392, 10.1002/9783527618460.
- Miron Ya. Amusia; Konstantin G. Popov; Vasily R. Shaginyan; Vladimir A. Stephanovich; Theory of Heavy-Fermion Compounds. Miron Ya. Amusia; Konstantin G. Popov; V.R. Shaginyan; Vladimir A. Stephanovich; Theory of Heavy-Fermion Compounds. Springer Series in Solid-State Sciences 2015, 182, 359, 10.1007/978-3-319-10825-4.
- V. A. Khodel; J. W. Clark; M. V. Zverev; Topological disorder triggered by interaction-induced flattening of electron spectra in solids. Physical Review B 2020, 102, 201108(R), , 201108, 10.1103/physrevb.102.201108.