Tunnel Boring Machines (TBMs) typically consist of a rotating cutter head that breaks up the rock or soil and a conveyor system that removes the excavated material. TBMs are preferred over traditional drill and blast techniques due to their higher efficiency, safer working conditions, minimal environmental disturbance, and reduced project costs. TBMs have become prevalent in tunnel construction due to their high efficiency and reliability. The proliferation of data obtained from site investigations and data acquisition systems provides an opportunity for the application of machine learning (ML) techniques. ML algorithms have been successfully applied in TBM tunneling because they are particularly effective in capturing complex, non-linear relationships.
- tunnel boring machine
- machine learning
- TBM performance
- surface settlement
- time series forecasting
1. Introduction
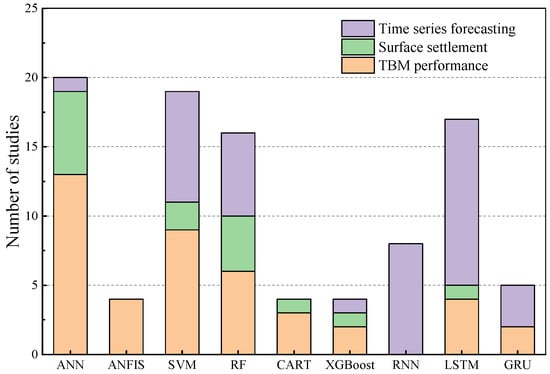
2. TBM Performance
| Literature | Data Processing a | Algorithms b | Hyperparameter Tuning c |
Targets d | Data Size and Data Set |
|---|
| Model Type | Dataset | Data Size | Parameters | Open Access | Limitations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grima et al. [6][26] | PCA | MR, ANN, ANFIS | - | Operational parameters,PR, AR | 640 tunnel project | |||||||||
| Guo et al. [57 | TBM type and size | No | ][20 | hard to access | ] | WT | Elman RNN | PSO | longitudinal settlement | Benardos and Kaliampakos [7][31] | - | ANN | - | |
| Jiangji subway tunnel | Model B | Queen water tunnel | AR | 11-Athens metro | ||||||||||
| 151 | Geological conditions | S(X) | ||||||||||||
| Zhang et al. [58][79 | 432-Toulouse subway line B | Tiryaki [8][28 | ||||||||||||
| ] | WT | ANN, SVM | - | daily settlement | 60-Wuhan metro line 2 | ] | PCA | MR, ANN | - | specific energy | 44-Three tunnel projects | |||
| Pourtaghi and Lotfollahi-Yaghin [46][33] | - | Wavelet-ANN | - | |||||||||||
| Gao et al. [59][37] | S | max | 49-Bangkok subway project | |||||||||||
| - | RNN, LSTM, GRU, SVM. RF, Lasso | - | TO, TH, AR, CP | 3000-Shenzhen metro | Mikaeil et al. [9][41] | Dindarloo and Siami-Irdemoosa [47]- | [76FL | ] | PCC- | Penetrability | 151-Queens water tunnel | |||
| CART | - | S | max | 34-Various tunnel projects | ||||||||||
| Zhou et al. [60][23] | WT | ARIMA, LSTM, CNN-LSTM | - | HDSH, HDST, VDSH, VDST, roll, pitch |
5005-Sanyang Road Tunnel | Yagiz [10][59] | PCC | MR, ANN | - | Goh et al. [48][77]PR | -151-Queens water tunnel | |||
| MARS | ||||||||||||||
| Gao et al. [61][80 | - | S | max | 148-Three Singapore MRT projects | Javad and Narges | |||||||||
| ] | 3-sigma rule, MA, GRG | GRU | genetic algorithm | earth pressure | 1538-Luoyang metro line 2 | [11][60] | - | ANN | - | PR | 185-Three tunnel projects | |||
| Chen et al. [49][24] | PCC | |||||||||||||
| Erharter and Marcher [ | ANN, RBF, GRNN | 62][ | - | Smax | 200-Changsha metro line 4 | |||||||||
| 81] | PCC | LSTM, RF, SVM | - | TO | 200,000-Brenner base tunnel | Mahdevari et al. [12][43] | - | MR, SVM | - | PR | 151-Queens water tunnel | |||
| Zhang et al. [20][47] | PCC | |||||||||||||
| Feng et al. | RF | [1] | PSO | Smax | 294-Changsha metro line 4 | |||||||||
| [13] | 3-sigma rule, WT | DBN | - | FPI | 8915-Yingsong water diversion project | Salimi et al. [ | Zhang et al. [50][34] | PCC | ANN, SVM, RF, EML, GRNN | PSO | Smax | 294-Changsha metro line 4 | ||
| Gao et al. [63][82] | - | ARIMA, RNN, LSTM | - | PR | Hangzhou second water source project | Zhang et al. [25][22] | WT, MD, GRG | LSTM, RF | PSO | Smax | 423-Changsha metro line 4 | |||
| Li et al. [64] | Zhang et al. [51][78] | PCC | XGBoost, ANN, SVM, MARS | - | Smax | 148-Three Singapore MRT projects | ||||||||
| Kannangara et al. [52][46] | PCC, sequential feature selection, Boruta algorithm | RF | - | Smax | 264-Hangzhou metro line 2 and line 6 |
4. Time Series Forecasting
Time series forecasting is a real-time prediction using current and historical data to forecast future unknown values, which means input parameters are available and it does not have the practical problem of Model C. It is crucial in TBM tunnelling for predicting TBM performance, surface settlement, and moving trajectory in real time because operators can make necessary adjustments when potential issues are detected. Several studies using ML techniques for time series forecasting are shown in Table 4. Since the quality and quantity of data heavily influence model performance, moving average or wavelet transform are employed to eliminate noise and fine-grained variation to reveal the underlying information in time series data [53][54][55][56][14,17,19,21].| Literature | Data Processing a | Algorithms b | Hyperparameter Tuning | Targets c | Data Size and Data Set |
|---|---|---|---|---|---|
| [ | |||||
| 2 | |||||
| ] | |||||
| PCC | |||||
| LSTM | |||||
| - | TO, TH | 4650-Yingsong water diversion project | |||
| Qin et al. [65][36] | cosine similarity | CNN-LSTM, XGBoost, RF, SVM, LSTM, RNN, CNN | - |
| Literature | Category | Historical Data | Forecast Horizon | |||||
|---|---|---|---|---|---|---|---|---|
| Step behind | Distance behind | Step ahead | Distance ahead | |||||
| Gao et al. [59][37] | high-frequency | 5 steps | 1.25 mm a | 1 step | 0.25 mm a | |||
| Qin et al. [65][36] | 10 steps | - | 1 step | - | ||||
| Huang et al. [68][53] | 6 steps | 22.4 mm a | 1 step | 3.73 mm a | ||||
| Erharter and Marcher [62][81] | 50 steps | 2.75 m | 1 or 100 steps | 0.055 or 5.5 m | ||||
| Shi et al. [66][39] | 10 steps | - | 1–5 steps | - | ||||
| Gao et al. [61][80] | low-frequency | 5 steps | 7.5 m | 1 step | 1.5 m | |||
| Feng et al. [1][13] | 7 steps | 7 m | ||||||
| TO | ||||||||
| 150,000-Singapore metro T225 project | ||||||||
| 1 step | 1 m | 13][27] | PCA | MR, SVM, ANFIS | - | FPI | 75-Zagros lot 1B and 2 | |
| Armaghani et al. [14][30] | - | ANN | PSO, ICA | PR | 1286-Pahang-Selangor raw water transfer | |||
| Yes | overfitting or lack of generalisability | Armaghani et al. [15][61] | - | MR, GEP | - | PR | 1286-Pahang-Selangor raw water transfer | |
| Sun et al. [16][18] | Kriging interpolation, rate of change | RF | - | TH, TO, PR | 88-Shenzhen metro | |||
| Armaghani et al. [17][55] | - | ANN | PSO, ICA | AR | 1286-Pahang-Selangor raw water transfer | |||
| Koopialipoor et al. [18][62] | - | ANN, DNN | - | PR | 1286-Pahang-Selangor raw water transfer | |||
| Salimi et al. [19][48] | PCA | MR, CART, GP | - | FPI | 580-Seven tunnel projects | |||
| Zhang et al. [20][47] | PCC | RF | PSO | TO, TH, PR, FP | 294-Changsha metro line 4 | |||
| Koopialipoor et al. [21][63] | - | ANN | firefly algorithm | PR | 1200-Pahang-Selangor raw water transfer | |||
| Mokhtari and Mooney [22][44] | PCC, Relief | SVM | BO | PR | Northgate Link tunnel | |||
| Wang et al. [23][64] | - | ANN, LSTM, RF, SVM | - | AR | 806-Nanning metro line 1 | |||
| Zhang et al. [24][49] | - | SVM, CART, RF, bagging, Ada boosting | BO | PR | 151-Queens water tunnel | |||
| ] | WT, MD, GRG | LSTM, RF | PSO | TH, TO, PR, RPM, CP | ||||
| Model C | Pahang-Selangor raw water transfer | 1286 | Geological conditions, Operational parameters |
3549-Changsha metro line 4 and Zhengzhou metro line 2 | ||||
| Zhang et al. [ | Zhou et al. [26][65] | - | ANN, GP | - | AR | 1286-Pahang-Selangor raw water transfer | ||
| Bai et al. [27][45] | PCC, Seasonal-trend decomposition | MR, SVM, DT, GBoost | - | TO, TH, FP | 450-Xi’an metro | |||
| Bardhan et al. [28][66] | - | hybrid ensemble model | - | PR | 185-Three tunnel project | |||
| Harandizadeh et al. [29][56] | - | ANFIS-PNN | ICA | PR | 209-Pahang-Selangor raw water transfer | |||
| Lin et al. [30][67] | - | MR, ANN, SVM, LSTM, GRU, EML | PR | 1000-Shenzhen railway | ||||
| Parsajoo et al. [31][42] | - | ANFIS | artificial bee colony | FPI | 150-Queens water tunnel | |||
| Zeng et al. [32][35] | - | EML | PSO | AR | 1286-Pahang-Selangor raw water transfer | |||
| Zhou et al. [33][54] | - | XGBoost | BO | AR | 1286-Pahang-Selangor raw water transfer | |||
| Zhou et al. [34][50] | - | ANN, RF, XGBoost, SVM | GWO, PSO, SCA, SSO, MVO, MFO | PR | 1286-Pahang-Selangor raw water transfer | |||
| Lin et al. [4][25] | - | LSTM | PSO | TH | 1500-Shenzhen railway | |||
| Lin et al. [35][68] | - | GRU | PSO] | - | MR, CART | - | FPI | 666-Eight tunnel projects |
| Model A | 640 tunnel projects | - | Geological conditions, | |||||
| TO | ||||||||
| 1500-Shenzhen railway | ||||||||
| Yes | hard to apply in practice | |||||||
| 25 | ||||||||
| ] | ||||||||
| [ | ||||||||
| 22 | ||||||||
| Salimi et al. | ||||||||
| [ | ||||||||
| 36 | ||||||||
| ] | ||||||||
| [ | ||||||||
| 69 | ||||||||
| Yang et al. | ||||||||
| [ | ||||||||
| 37 | ||||||||
| ] | ||||||||
| [ | ||||||||
| 3 | ||||||||
| ] | ||||||||
| - | ||||||||
| SVM | ||||||||
| GWO, biogeography-based optimisation | ||||||||
| PR | 503-Shenzhen metro line |
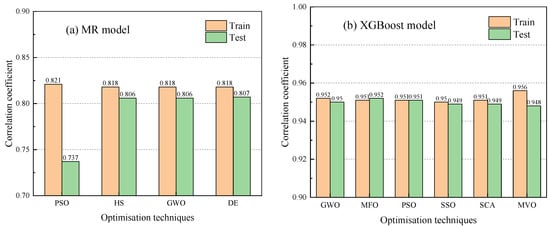
3. Surface Settlement
The surface settlement, the subsidence of the ground surface above a tunnel due to excavation, poses risks to surrounding structures and utilities. Accurate prediction of surface settlement is essential for mitigating potential damages during tunnel construction. Engineers can minimise ground movement and reduce the risk of damage by adjusting excavation parameters and support structures. Table 3 reviews papers on settlement induced by TBM tunnelling and excludes construction methods such as drilling, blasting, and the new Austrian Tunnelling Method [41][42][43][72,73,74].| Literature | Data Processing | Algorithms a | Hyperparameter Tuning | Targets | Data Size and Data Set | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Suwansawat and Einstein [44][32] | - | ANN | - | Smax | 49-Bangkok subway project | |||||
| Boubou et al. [45][75] | - | ANN | - | |||||||
| Shi et al. | ||||||||||
| [ | ||||||||||
| 66 | ||||||||||
| ] | ||||||||||
| [ | ||||||||||
| 39 | ||||||||||
| ] | ||||||||||
| WT, variational mode decomposition | LSTM, CNN, RNN, SVM, RF | - | TO | 60,000-Singapore metro T225 project | ||||||
| Wang et al. [56][21] | WT, light gradient boosting machine | LSTM | - | PR, TO | 25,543-Sutong gas transmission line | |||||
| Xu et al. [53][14] | 3-sigma rule, MA, PCC | SVM, RF, CNN, LSTM, GBoost, KNN, Bayesian ridge regression | - | PR, TO, TH, RPM | 7000-Yingsong water diversion project | |||||
| 463-Changsha metro line 4 and Zhengzhou metro line 2 | ||||||||||
| Shen et al. [54 | ||||||||||
| Shan et al. [55][19] | 5 steps | 7.5 m | 1–5 steps | Zhang et al. [67][83] | - | RF | - | Smax | 386-Changsha Metro Line 4 | |
| Huang et al. [68][53] | SelectKBest | LSTM | BO | TO | Yingsong water diversion project | |||||
| 1.5–7.5 m | Shan et al. [55][19] | MA | RNN, LSTM | - | PR][17] | WT, Kriging interpolation | LSTM, SVM, RNN | - | HDSH, HDST, VDSH, VDST, roll, pitch | 1200-Shenzhen intercity railway |
| Zhang et al. [5][29] | PCA, PCC | GRU, RNN, SVM | - | HDSH, HDST, VDSH, VDST, | 22,010-Guang-Fo intercity railway |
