A common feature of tumor pathological metabolism is an increased glucose uptake, together with its fermentation to lactate, even under aerobic conditions. This behavior is known as Warburg effect. 2-deoxy-2-[18F]fluoro-D-glucose (FDG) is a glucose analog that is systematically utilized as a radioactive tracer in nuclear medicine. FDG Positron Emission Tomography (FDG-PET) is a functional imaging modality that utilizes FDG as a tracer in order to quantitative assess FDG metabolism in tumors (but other pathologies are systematically investigated as well, by means of this imaging technique). FDG-PET measures the radiation emitted by the tracer injected in the organism, and these measurements encode, in a very indirect way, two kinds of information: the localization of FDG accumulation in the body and the rate with which FDG changes its metabolic status along time. In order to decode such sophisticated information, two inverse problems must be solved: (1) Image reconstruction inverse problem: to reconstruct the spatio-temporal distribution of FDG inside the tissue by solving the integral equation that connects the FDG density to the measured radiation by means of the Radon transform. (2) Compartmental inverse problem: to model the tracer kinetics by solving the non-linear time-dependent equation that connects the tracer coefficients to the reconstructed FDG concentration.
- Positron Emission Tomography (PET)
- FDG
- tracer kinetics
- compartmental analysis
1. The Experimental Data in the Compartmental Game
Solid tumors present an increase of the glucose consumption that occurs even under aerobic conditions [1]. This mechanism is known as the Warburg effect, and its origin is still unknown, although several studies have shown a significant correlation between glucose consumption and tumor aggressiveness. From an experimental viewpoint, it is very difficult to directly measure the flux of glucose molecules through biological tissues populated by cancer cells; however, the peculiar kinetic features of a glucose analog, the 2-[18F]-2deoxy-D-glucose (FDG), allow a reliable estimate of such parameter. Indeed, FDG is transported through cell membranes by the same GLUT transporters as glucose, and it is trapped in the cytosol by phosphorylation catalyzed by the same hexokinases. However, differently from glucose-6-phosphate (G6P), FDG6P is a false substrate for downstream enzymes channeling G6P to glycolysis or the pentose-phosphate pathway. Thus, FDG6P accumulates in cells and tissues, and its amount is considered an accurate marker of their overall glucose consumption[2][3][4]. Accordingly, the measured tracer content may be employed in non invasive cancer detection and staging, and in the assessment of drug treatments.
In vivo, cancer FDG uptake depends on the glucose level in the blood[5][6], on the possible administered drugs[7], and on the amount of the available tracer, which in turn is related to the diffusion processes occurring in the whole body after injection. Further, tracer concentration in the blood is a time-dependent parameter, as a consequence of several factors, such as absorption by the brain[8], urinary elimination[7], accumulation in liver[9], and the different accumulation rates of the various tissues[10].
In Positron Emission Tomography (PET), the tracer is injected into the subject via intravenous administration, and gamma-ray detectors measure the radiation emitted in vivo by the target tissue. This device is calibrated in such a way that imaging procedures allow the reconstruction of the tracer distribution in the body. The reconstructed activity concentration may depend on both a specific region of interest at a chosen time, and on the time course in a given time interval, where the time variable t is measured in minutes from the time of the tracer injection.
In this section we recall a few essential features of the sources of data providing the input for kinetic models of tracer dynamics. We consider first the standardized uptake value (SUV), which approximates the tracer metabolic assessment by using a single time frame (static imaging); next we consider (dynamic) estimates of the time course of tracer concentration in blood (input function) and tracer concentration in the target tissue, which are both obtained from a time series of images.
1.1. Standardized Uptake Value
Perhaps, the standardized uptake value (SUV) is the simplest parameter which is used to quantify tracer accumulation from reconstructed PET images. First, the concentration of tracer emitters in a region of interest (ROI) of the target tissue is recovered at a given time, as the solution of an appropriately defined inverse problem. Next, the corresponding normalized radioactivity concentration is estimated by the SUV, which is defined as[11]
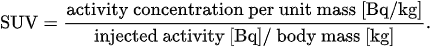
According to this definition, the radioactivity concentration in the ROI is normalized to the radioactivity concentration in the body, which is estimated as the ratio between the injected activity and the patient body mass. There are slightly different definitions available; moreover, SUV measurements are affected by physiological and technological factors[10][11].
Overall, the SUV is an oversimplified index depending on the time interval between injection and observation, location and dimensions of the ROI, and uptake by other tissues[10]. Nevertheless, the localized SUV has been used to stage tumors and to assess response to therapies.
1.2. Input Function
Tissues extract the tracer from blood. Indeed, only free FDG is available for tissue uptake, while the radioligand bound to blood cells and metabolites is firmly constrained to remain in blood[12][13]. In the present work, the concentration Cb of the tracer available for input to tissues is identified with the measured concentration in arterial blood, which means in particular that the bound tracer is disregarded. Considerations about bound tracer are discussed in Reference[13].
Tracer is delivered to tissues via blood flow, so that the amount of tracer locally extracted by a tissue is highly dependent on the concentration of radioactivity in blood. Thus, the reconstruction of FDG kinetics requires the knowledge of the arterial plasma time-activity concentration curve of the tracer, which in turn provides an estimate of the radioactivity available for uptake. There are several ways for the determination of the time course of concentration: serial arterial sampling, which is independent of PET data acquisition; images of tracer concentration in blood pools[14], such as the left ventricle; a variety of statistical reconstruction methods[15].
In the present work, the arterial plasma activity concentration curve is regarded as given and plays the role of input function (IF). We assume that the IF, as well as any other activity curve, has been corrected for tracer decay.
1.3. Activity Concentration of Target Tissue
The target tissue (TT) is the tissue selected for measuring the activity concentration Ct [kBq/mL]. Specifically, the tissue response is the time course of Ct , which is computed by realizing a ROI-based analysis of a dynamical series of reconstructed PET images[2][16]. Of course, these data are corrected for attenuation and possible systematic errors, and the resulting Ct depends on several factors like the injected dose, the shape of the IF, the characteristics of the TT, and the pato-physiological conditions of the patient.
We point out that the activity concentration measured by a PET device is the superposition of different signals: the one emitted by tracer molecules in the blood that occupies the ROI volume, the one associated to the tracer in the interstitial volume, and the one emitted by the FDG molecules phosphorylated in the cell. The analysis of these PET data aims at the reconstruction of the detailed kinetics of the tracer. In a sense, the measured signal has to be resolved into the activity pertaining to each source. To this aim, tracer kinetics takes into account the flow of radioactive molecules between the various sources. This is achieved by the application a mathematical models, as described in the next section. Comparison between model predictions and measured data leads to the determination of tracer kinetics, through solution of an inverse problem.
2. The Construction of Compartmental Models
2.1. Generalities
Compartmental models relate the measured dynamical PET data to either specific metabolic states or tracer chemical compounds, also accounting for their distribution in space. These functional states are known as compartments (or also as sources, or pools). Compartmental analysis relies on the so-called well-mixed assumption, stating that the tracer distribution in each compartment must be considered as homogeneous, and the tracer is instantaneously mixed when it is exchanged between compartments. A discussion of further assumptions will be described in detail in the next subsection.
In the framework of compartmental analysis, compartments have specific functional meanings and are characterized by specific time-dependent tracer concentrations. Therefore, different compartments may occupy the same spatial volume as typically occurs, for instance, in the case of free and phosphorylated FDG molecules. Conversely, a specific chemical compound may be associated to multiple spatially distinguished compartments and, in them, it may be characterized by different concentrations.
A compartmental model is a set of interconnected compartments, whose number depends on the chemical, physiological, and biological properties of the tracer[17][2][18]. In the compartmental framework, a biological system with complex physiological properties is approximated by a limited number of basic functional constituents. In this context, even the blood could be regarded as a compartment; however, in this review, we will assume that the tracer concentration in the blood is known and provided by ad hoc measurements[16].
The concentrations of the various pools are the state variables of the CM, their time dependence being determined by tracer exchange. The tracer flux between compartments, e.g., from the free to the phosphorylated pool, occurs according to mass conservation. Usually, it is assumed that the outgoing flux depends on the concentration of the source.
Assuming that the conservation of the tracer concentration occurs implies that the time rate of the tracer concentration for each compartment is given by the difference between the amount of tracer entering the pool and the amount of tracer leaving the same pool, per unit time and unit volume. This assumption, therefore, leads to a system of ordinary differential equations (ODEs), in which the IF providing the tracer supply to the compartments represents the forcing function of the system. We also assume that all the initial concentrations are zero, i.e., that there is no tracer available to the tissue at the starting point of the experiment. In the resulting mathematical model, the state variables represent the solutions of the Cauchy problem, which is made of linear ODEs with constant and homogeneous rate coefficients (also named transfer coefficients or microparameters) representing the rate of tracer flux between compartments, i.e., the phosphorylation rate for the FDG molecules[19]. Given the rate coefficients and the initial state, the numerical solution of the Cauchy problem describes the tracer kinetics. However, in compartmental analysis, the rate coefficients are unknown and must be determined in such a way that the resulting estimates are in accordance with the measured overall tissue concentration. Therefore, the compartmental problem is intrinsically a non-linear inverse problem, and the first step for its solution is the proof that these rate coefficients can be uniquely determined from the measured data. This need implies a limitation on the number of microparameters and, in turn, on the number of functional compartments. The result of this approach is a trade-off between an exhaustive accordance to reality, and the need of simplifying the formal description and the corresponding system of equations.
2.2. Basic Applicability Conditions
In a typical PET experiment, a fraction of tracer is adsorbed by tissues after injection into blood, while some tracer is lost by tissues and poured back into blood. The previous discussion has indicated that application of compartmental analysis allows a reliable reconstruction of tracer kinetics, but this can be achieved only if a certain number of conditions are satisfied in the course of the experiment[2][3][12][16][20]. The following list describes the most common and relevant requirements.
-
Tracer is administered in trace amounts. The number of injected molecules is supposed to be sufficiently high so that diffusion may described by application of a continuous model. However, such a number is not so high as to influence physiological processes and molecular interactions. In particular, tracer does not affect glucose metabolism.
-
During an experiment, physiologic conditions are in a steady state which is not affected by measurement devices of tracer concentration. This holds true, in particular, for glucose metabolism.
-
The well-mixing condition holds for each compartment. In practice, this means that equilibrium is reached in a time interval, which is rather short with respect to the time of data acquisition. As a consequence, the spatial homogeneity condition follows, which implies that the tracer concentration in each compartment depends only on time.
-
Transport of tracer molecules and related composites between compartments follows a first order kinetics, which ultimately leads to linear ODEs.
-
Bound tracer in blood is disregarded, and the arterial concentration of tracer available for tissue uptake is regarded as a valuable approximation of capillary concentration.
We have described general assumptions underlying most used compartmental models. More specific aspects of tracer kinetics may be considered in order to generate highly realistic models. For example, a distinction may be introduced between free interstitial tracer and free intracellular tracer; permeabilities of blood vessels and cellular membranes may be considered, as well as dependence of activity on spatial variables. CMs explicitly devoted to the modeling of particular physiologic conditions will be examined in a subsequent section.
2.3. Examples
Figure 1 depicts a standard 2-compartment model (2-CM) that has been used to model the intracellular processes of phosphorylation and dephosphorylation of FDG through two compartments, Cf and Cp , accounting for free and phosphorylated tracers, respectively[16][21].
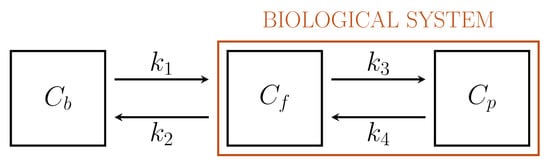
Figure 1. Standard Sokoloff’s 2-compartment model.
Biochemistry explains that the endoplasmic reticulum (ER)[22] plays a crucial role in the activation of G6Pase and that, specifically, the hydrolysis of G6P and FDG6P with the corresponding creation of free glucose and FDG molecules and a phosphate group occurs after the transmembrane protein glucose-6-phosphate transporter (G6PT) transports the phosphorylated forms into ER[23]. After this process, free FDG can be released into the cytosol. This argument and further biochemical, pharmacological, clinical, and genetic data implies the interpretation of ER as a specific functional compartment[24].
Driven by biochemical reactions involving FDG molecules, a 3-compartment model (3-CM) has been developed, which is formed by the following compartments: Cf , accounting for free tracer in the cytosol and possibly in the interstitial space, Cp for phosphorylated FDG in cytosol, and Cr for phosphorylated FDG in ER[6][25]. The resulting compartment model is depicted in Figure 2. The standard compartmental 2-CM is recovered from the 3-CM under the assumption that the ER compartment is removed.
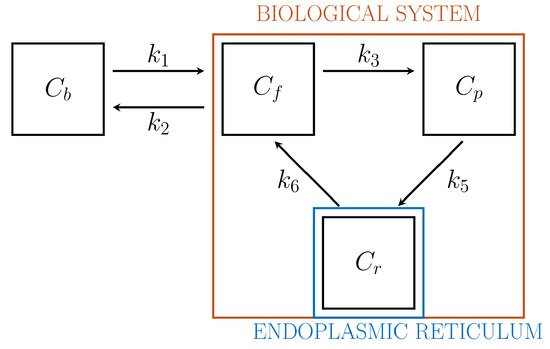
Figure 2. 3-compartment model for cell absorption.
In our paper we also review a number of more complex, biologically-driven comparment models, specifically devised to model FDG kinetics in a reference tissue[26], in the liver[9], and in the renal system[7][27].
3. Some Numerics: Optimization Schemes
In experimental applications, the input data is given by the time series CT =CT(t) , which is determined by computing the pixel content in Regions of Interest (ROIs) of the reconstructed PET data at different time points; Cb =Cb(t) is the input function, which is also determined from PET data; and the unknown is represented by the vector k, whose components are the tracer coefficients, and byVb , the volume fraction of tissue occupied by blood. We define
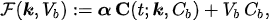
where α is a constant row vector of order n, with components possibly depending on the physiological parameters. The computational problem of compartmental analysis is the one to determine, at each time point,
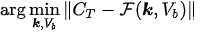
In this optimization equation, || · || denotes the topology with which the distance between the experimental and predicted total concentrations is measured. Naive approaches to the computational solution of such a problem are typically characterized by three
main drawbacks:
-
They typically suffer numerical instabilities related to the non-uniqueness and sensitivity limitations.
-
They may suffer local minima as the operator F is non linear and the space where possible minimizers can be searched for is typically big.
-
Particularly, in the case of three-compartment models, the number of kinetic parameters to determine is high, which implies that they are computationally demanding.
Several numerical methods have been applied for the solution of the comparment inverse problem, whose reliability and computational effectiveness depend on the choice of the topology || · || and
by the way possible prior information on the solution are encoded in the optimization process. Further, the computational algorithms utilized for solving the minimization problem typically belong to three general approaches: the deterministic, statistical, and biology-inspired ones. In our review, we provide a sketch of the main computational aspects of these three approaches, assuming that Vb is known thanks to either experimental or physiological information (the generalization to the case when also Vb is an unknown parameter is straightforward).
In order to show how some of these methods behave in action, Figure 3 summarizes some results obtained in the literature by using experimental measurements recorded by means of a PET scanner for small animals.
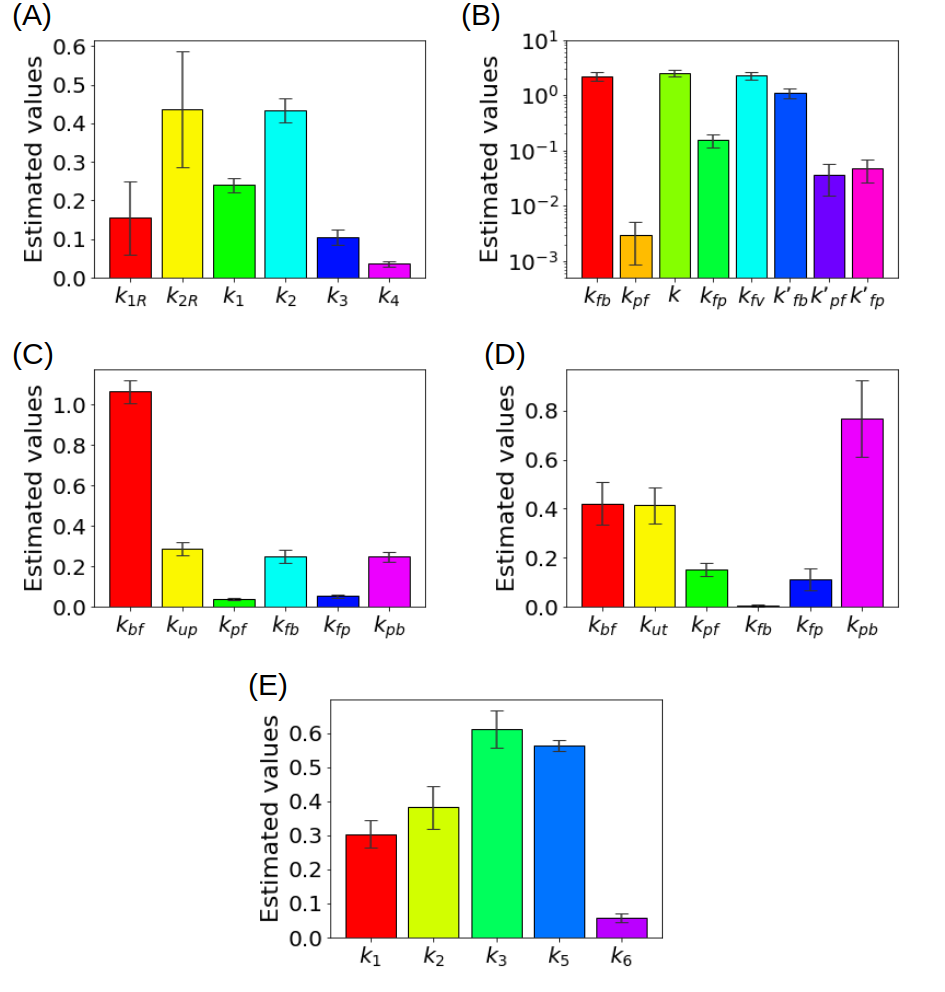
Figure 3. (A) Kinetic parameters estimated for the reference tissue CM with a deterministic approach (B) Kinetic parameters estimated for the liver CM with a deterministic approach (C) Kinetic parameters for a simplified CM for the renal system estimated with ant colony optimization, (D) Kinetic parameters for the CM of the renal system estimated with a statistical approach (E) Kinetic parameters of the CM including the endoplasmic reticulum estimated with a regularized Gauss-Newton approach.
A a Matlab package equipped with a user-friendly graphical user interface (GUI) for the analysis of different compartmental models, namely standard 2-CM, kidney, and liver, is available at https://github.com/theMIDAgroup/ CompartmentalAnalysis. Similarly, a Matlab package for analyzing a compartmental system based on reference tissue modeling is available at https://github.com/theMIDAgroup/ReferenceTissue_CompartmentalAnalysis, while the github repository https://github.com/theMIDAgroup/BCM_CompartmentalAnalysis contains the Matlab code for the analysis of the 3-CM accounting for the endoplasmic reticulum.
34. Conclusion
Compartmental analysis is a well-established approach to the interpretation of dynamical FDG-PET data and this review paper has aimed to point out the fact that numerical algorithms for the reduction of compartmental models play a crucial role for the comprehension of cancer glucose metabolism from a quantitative viewpoint. Yet, some technical issues are still open, whose solution would imply a further significant improvement in the comprehension of glucose dynamics in cancerous tissues.
References
- Vander Heiden, M.G.; Cantley, L.C.; Thompson, C.B. Understanding the Warburg effect: The metabolic requirements of cell proliferation. Science 2009, 324, 1029–1033.
- Cherry, S.R.; Sorenson, J.A.; Phelps, M.E. Physics in Nuclear Medicine; Elsevier Health Sciences: Amsterdam, The Netherlands, 2012.
- Muzi, M.; Freeman, S.D.; Burrows, R.C.; Wiseman, R.W.; Link, J.M.; Krohn, K.A.; Graham, M.M.; Spence, A.M. Kinetic characterization of hexokinase isoenzymes from glioma cells: Implications for FDG imaging of human brain tumors. Nucl. Med. Biol. 2001, 28, 107–116.
- Maddalena, F.; Lettini, G.; Gallicchio, R.; Sisinni, L.; Simeon, V.; Nardelli, A.; Venetucci, A.A.; Storto, G.; Landriscina, M. Evaluation of glucose uptake in normal and cancer cell lines by positron emission tomography. Mol. Imag. 2015, 14, 490–498.
- Williams, S.P.; Flores-Mercado, J.E.; Port, R.E.; Bengtsson, T. Quantitation of glucose uptake in tumors by dynamic FDG-PET has less glucose bias and lower variability when adjusted for partial saturation of glucose transport. Eur. J. Nucl. Med. Mol. Imag. Res. 2012, 2, 1–13.
- Scussolini, M.; Bauckneht, M.; Cossu, V.; Bruno, S.; Orengo, A.M.; Piccioli, P.; Capitanio, S.; Yosifov, N.; Ravera, S.; Morbelli, S.; et al. G6Pase location in the endoplasmic reticulum: Implications on compartmental analysis of FDG uptake in cancer cells. Sci. Rep. 2019, 9, 1–14.
- Garbarino, S.; Caviglia, G.; Sambuceti, G.; Benvenuto, F.; Piana, M. A novel description of FDG excretion in the renal system: Application to metformin-treated models. Phys. Med. Biol. 2014, 59, 2469.
- Signorini, M.; Paulesu, E.; Friston, K.; Perani, D.; Colleluori, A.; Lucignani, G.; Grassi, F.; Bettinardi, V.; Frackowiak, R.; Fazio, F. Rapid assessment of regional cerebral metabolic abnormalities in single subjects with quantitative and nonquantitative [18F]FDG PET: A clinical validation of statistical parametric mapping. Neuroimage 1999, 9, 63–80.
- Garbarino, S.; Vivaldi, V.; Delbary, F.; Caviglia, G.; Piana, M.; Marini, C.; Capitanio, S.; Calamia, I.; Buschiazzo, A.; Sambuceti, G. A new compartmental method for the analysis of liver FDG kinetics in small animal models. EJNMMI Res. 2015, 5, 35.
- Büsing, K.A.; Schönberg, S.O.; Brade, J.; Wasser, K. Impact of blood glucose, diabetes, insulin, and obesity on standardized uptake values in tumors and healthy organs on 18F-FDG PET/CT. Nucl. Med. Biol. 2013, 40, 206–213.
- Adams, M.C.; Turkington, T.G.; Wilson, J.M.; Wong, T.Z. A systematic review of the factors affecting accuracy of SUV measurements. AJR Am. J. Roentgenol. 2010, 195, 310–320.
- Schmidt, K.C.; Turkheimer, F.E. Kinetic modeling in positron emission tomography. Quart J. Nucl. Med. 2002, 46, 70–85.
- Schain, M.; Fazio, P.; Mrzljak, L.; Amini, N.; Al-Tawil, N.; Fitzer-Attas, C.; Bronzova, J.; Landwehrmeyer, B.; Sampaio, C.; Halldin, C.; et al. Revisiting the Logan plot to account for non-negligible blood volume in brain tissue. Eur. J. Nucl. Med. Mol. Imag. Res. 2017, 7, 1–12.
- Zanotti-Fregonara, P.; Chen, K.; Liow, J.S.; Fujita, M.; Innis, R.B. Image-derived input function for brain PET studies: Many challenges and few opportunities. J. Cer. Blood Flow Metab. 2011, 31, 1986–1998.
- Vriens, D.; de Geus-Oei, L.F.; Oyen, W.J.; Visser, E.P. A curve-fitting approach to estimate the arterial plasma input function for the assessment of glucose metabolic rate and response to treatment. J. Nucl. Med. 2009, 50, 1933–1939.
- Wernick, M.N.; Aarsvold, J.N. Emission Tomography: The Fundamentals of PET and SPECT; Elsevier: Amsterdam, The Netherlands, 2004.
- Watabe, H.; Ikoma, Y.; Kimura, Y.; Naganawa, M.; Shidahara, M. PET kinetic analysis–compartmental model. Ann. Nucl. Med. 2006, 20, 583–588.
- Lawson, R.S. Application of mathematical methods in dynamic nuclear medicine studies. Phys. Med. Biol. 1999, 44, R57–R98.
- Gunn, R.N.; Gunn, S.R.; Cunningham, V.J. Positron emission tomography compartmental models. J. Cer. Blood Flow Metab. 2001, 21, 635–652.
- Bertoldo, A.; Rizzo, G.; Veronese, M. Deriving physiological information from PET images: From SUV to compartmental modelling. Clin. Transl. Imaging 2014, 2, 239–251.
- Sokoloff, L.; Reivich, M.; Kennedy, C.; Rosiers, M.D.; Patlak, C.; Pettigrew, K.E.A.; Sakurada, O.; Shinohara, M. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: Theory, procedure, and normal values in the conscious and anesthetized albino rat. J. Neurochem. 1977, 28, 897–916.
- Ghosh, A.; Shieh, J.J.; Pan, C.J.; Sun, M.S.; Chou, J.Y. The catalytic center of glucose-6-phosphatase. HIS176 is the nucleophile forming the phosphohistidine-enzyme intermediate during catalysis. J. Biol. Chem. 2002, 277, 32837–32842.
- Marini, C.; Ravera, S.; Buschiazzo, A.; Bianchi, G.; Orengo, A.M.; Bruno, S.; Bottoni, G.; Emionite, L.; Pastorino, F.; Monteverde, E.; et al. Discovery of a novel glucose metabolism in cancer: The role of endoplasmic reticulum beyond glycolysis and pentose phosphate shunt. Sci. Rep. 2016, 6, 1–13.
- Csala, M.; Marcolongo, P.; Lizák, B.; Senesi, S.; Margittai, É.; Fulceri, R.; Magyar, J.É.; Benedetti, A.; Bánhegyi, G. Transport and transporters in the endoplasmic reticulum. Biochim. Biophys. Acta Biomembr. 2007, 1768, 1325–1341.
- Sommariva, S.; Scussolini, M.; Cossu, V.; Marini, C.; Sambuceti, G.; Caviglia, G.; Piana, M. The role of endoplasmic reticulum in in vivo cancer FDG kinetics. PLoS ONE 2021, 16, e0252422.
- Scussolini, M.; Garbarino, S.; Piana, M.; Sambuceti, G.; Caviglia, G.; Reference tissue models for FDG-PET data: Identifiability and solvability. IEEE Trans. Rad. Plasma Med. Sci. 2018, 2, 177–186..
- Garbarino, S.; Caviglia, G.; Brignone, M.; Massollo, M.; Sambuceti, G.; Piana, M.; Estimate of FDG excretion by means of compartmental analysis and ant colony optimization of nuclear medicine data. Comput. Math. Methods Med. 2013, 2013, 793142.
- Scussolini, M.; Garbarino, S.; Piana, M.; Sambuceti, G.; Caviglia, G.; Reference tissue models for FDG-PET data: Identifiability and solvability. IEEE Trans. Rad. Plasma Med. Sci. 2018, 2, 177–186..
- Garbarino, S.; Caviglia, G.; Brignone, M.; Massollo, M.; Sambuceti, G.; Piana, M.; Estimate of FDG excretion by means of compartmental analysis and ant colony optimization of nuclear medicine data. Comput. Math. Methods Med. 2013, 2013, 793142.
