1000/1000
Hot
Most Recent

Prestressing methods were used to realize long-span bridges in the last few decades. For their maintenance, dynamic nondestructive procedures for identifying prestress losses were mainly developed since serviceability and safety of Prestressed Concrete (PC) girders depend on the effective state of prestressing. In fact, substantial long term prestress losses can induce excessive deflections and cracking in PC bridge girders. However, old unsolved problematics exist since a variation in prestress force does not significantly affect the vibration responses of such PC girders. As a result, this makes uncertain the use of natural frequencies as appropriate parameters for prestress loss determinations. Thus, amongst emerging techniques, static identification based on vertical deflections has preliminary proved to be a reliable method. In fact, measured vertical deflections take accurately and instantaneously into account the changes of structural geometry of PC girders due to prestressing losses. Given the current state of methodologies, the manuscript represents a state-of-the-art review of some important works on determining prestress losses. The attention is principally focused on a static nondestructive method, and a comparison with dynamic ones is elaborated.
The first applications of prestressing methods to concrete structures go back to the first half of the 20th century. Today prestressing is widely used for many applications, ranging from small members, such as railway sleepers, to more important structures such as bridges, long and light precast flooring, and roofing elements for constructions. Serviceability and safety of Prestressed Concrete (PC) structures rely on the effective state of prestress force [1]. In fact, prestressing methods are principally utilized to reduce deflections and to partially counterbalance the effect of dead and live loads in the case of bridges [2]. As a result, an extreme loss of prestressing may cause excessive deflections or jeopardize the performance of large span PC girders by indicating cracking phenomena [3]. For this reason, devices and dynamic approaches capable of determining prestress losses largely developed. In particular, dynamic Structural Health Monitoring (SHM) techniques also generated for damage identification purposes based on the vibration responses of the span girders, so preventing maintenance, repair, or replacement of a bridge [4][5][6]. Damage detection techniques as well developed using different equipment and methods as, e.g., parked vehicles inducing frequency variation [7], long-gauge Fiber Bragg Grating (FBG) [8], or hybrid vibration testing data [9]. Therefore, the operating state of bridges can be controlled. However, prestress losses can be directly, simply, and accurately determined over time if the internal tendons of PC girders are instrumented by load cells, vibrating wire strain gauges, or elasto-magnetic sensors during construction [10][11][12][13]. Besides, FBG sensors can be embedded in seven-wire strands along PC girders for long term monitoring of tensile forces [14][15]. Although instrumentation of external tendons is easy during their serviceability, NonDestructive Testing (NDT) methods are required. Nevertheless, as far as the influence of prestressing on the dynamics of PC girders is concerned, the discussion is still ongoing.
Several procedures and equations are available in design codes for predicting prestress losses. According to ACI 318-2019 [16] and PCI DH [17], reasonable estimations can be calculated. For unusual design conditions and special structures, a more detailed procedure established by PCI CPL [18] can be considered. AASHTO LRFD [19] adopted new procedures since the previous prestress loss methods led to unrealistic applications with high strength concrete. However, AASHTO Standard specifications [20] remain in accordance with AASHTO LRFD [21]. PCI BDM [22] includes both AASHTO Standard [20] and LRFD [21] methods.
A series of studies were conducted to measure prestress losses in PC girders, and to compare them versus design code estimations. Among these works, there are laboratory tests of old PC girders removed from existing bridges, and experiments including fabrication, testing, and field monitoring of PC members under service. Table 1 in [23] and Table 6 in [24] summarize an extensive literature review on references, PC member identification (type, old time), testing place, experimental technique used, time of study, and measured losses. As observed in these tables, measured prestress losses exceeded those predicted by design codes in some cases. On the other hand, measured prestress losses which were in line with the values expected by codes were obtained in PC girders, which exceeded the allowable compressive stress limit [25]. To overcome this problem, Caro et al. [26] used the ECADA+ method [27] to measure the effective prestress forces in a number of PC specimens for over 1 year and, consequently, compared the results with prestress losses estimated by several codes. Although design code-based predictions can be considered as quite satisfactory, they are very conservative [28]. Accordingly, there are difficulties in determining prestress losses related to factors including, inter alia, assumptions about the properties of prestressing systems and time-dependent phenomena, such as long term degradation processes, tendon relaxation, creep and shrinkage of concrete, and parameters of the real environment [29][30].
Given the current state of quantitative and principled methodologies, this paper represents a state-of-the-art review of some important research works conducted worldwide on determining prestress losses in PC girders. At first, laboratory, numerical investigations, and testing methods are reviewed. Secondly, the article focuses on a static NDT method, and a comparison with dynamic ones is elaborated, since old unsolved problematics as well as new challenges exist because a variation in prestress force does not significantly influence the vibration responses of PC girders. Consequently, this makes uncertain the use of natural frequencies as appropriate parameters for prestress loss determinations. Thus, amongst emerging techniques, static identification based on vertical deflections has preliminary proved to be a reliable method with the aim to become a dominant testing approach in the near future. In fact, measured vertical deflections take accurately and instantaneously into account the changes of structural geometry of PC girders due to prestressing losses on the equilibrium conditions, in turn caused by the combined effects of relaxation of tendon, concrete creep and shrinkage, and parameters of the real environment as, e.g., temperature and relative humidity. Comments and recommendations are made at proper places, whilst concluding remarks including future investigations and field developments are mentioned at the end of the article.
Amongst vibration-based techniques, static identifications using vertical deflections have proved to be reliable methods for axial force identification in beam elements. Indeed, measured vertical deflections take accurately into account the changes of structural geometry of the members due to axial force variations on the equilibrium conditions [31][32][33][34][35][36] (Figure 1a,b). Experimental simulations were as well conducted on members belonging to space frames and trusses [37][38][39]. Likewise, Bonopera et al. [40] verified the feasibility of estimating prestress force in a PC girder using vertical deflections measured by three-point bending tests. It is also worth noting that this approach only adopts static parameters, thus, in contrast to vibration-based techniques, does not require selecting experimental data for use in the algorithms.

Figure 1. Static NDT methods proposed by Tullini et al. [33][34]: (a) cast iron disks suspended at the reference beam; (b) arrangement of the dial indicators for vertical deflection measurements during an experimental simulation. Copyright © 2012, 2013 Elsevier Ltd. Reprinted with permission.
The static approach was originally developed for detecting axial force in compressed steel beams [35]. Subsequently, it was employed for identifying prestress forces in PC girders [40]. In this last case, the reference model comprised a simply supported Euler–Bernoulli beam of 250 mm in width, 400 mm in height, and length L of 6.62 m, made with a high strength concrete, and prestressed by a straight unbonded tendon, where the prestress force N was assumed as an external compressive force eccentrically applied to the end constraints N e (Figure 2a). The cross sectional second moment of the area of the PC beam’s section I was equal to 1.3333 × 109 mm4. Besides, a bending deflection v(1) along the aforementioned beam’s model, of 0.01 mm in accuracy, was properly approximated by multiplying the corresponding first-order deflection by the “magnification factor” of the second-order effects, id est, according to the “compression-softening” theory [31][32][41] (Figure 2b).
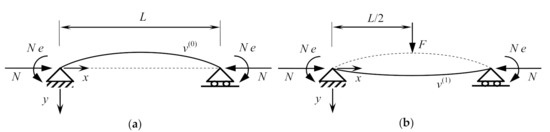
Figure 2. Reference model of the PC girder [80]: (a) deflection curve v(0) after the application of the eccentric prestress force N; (b) deflection curve v(1) after the application of the vertical load F to the deflection curve v(0). The dashed lines represent the initial deflection curves. Copyright © 2018, World Scientific Publishing Co. Pte Ltd. Reprinted with permission.
Experiments on a PC beam specimen, having the test configuration above mentioned (Figure 2a,b), were arranged in the laboratory of the National Center for Research on Earthquake Engineering (NCREE) of Taipei, Taiwan [40], where a research program, based on testing uncracked PC bridge member prototypes, began in 2015 (Figure 3). All geometrical dimensions were checked by laser rangefinder and caliper, of 0.01 mm in tolerance, after the PC beam was fixed on the simple supports. First, deflected-shape measurements v(1) along its span, obtained from 27 three-point bending tests with different applied prestress forces N, measured by a load cell placed at both end constraints [42], were examined to verify the accuracy of the assumptions of the beam’s model (Figure 2b). The span of the PC beam specimen was specifically instrumented to short term measure such static deflection shapes, with an accuracy of 0.01 mm, by a set of displacement transducers. Temperature and relative humidity of real environment of the PC beam were not continuously recorded during testing. Second, based on the “magnification factor” formula of the “compression-softening” theory [31][32][41], prestress force determinations were obtained using two series of vertical deflections v(1), id est, those recorded at the quarter v2(1) and at the midspan v4(1) of the PC beam, respectively. Information regarding the flexural rigidity of the PC beam were in addition required. In detail, average values of the chord elastic modulus Eaver of the high strength concrete, with an accuracy of 1 MPa, were estimated by compression tests on a series of cylinders cast at the same time of the PC beam [43] to determine its increment caused by the concrete’s consolidation/hardening with time [44].

Figure 3. Three-point bending tests on a PCI girder conducted in the laboratory of NCREE, Taiwan [45]: (a) indoor test rig; (b) application of a FBG-Differential Settlement Measurement (DSM) liquid-level system for vertical deflection measurements along the span. Copyright © 2019 Elsevier Ltd. Adapted with permission.
Table 1 lists the prestress force determinations Na obtained using the vertical deflections v2(1) and corresponding experimental values Ψ = F L3/Eaver I in Equation (8a) (Test 1), as well as the vertical deflections v4(1) and corresponding parameters Ψ in Equation (8b) (Test 2), respectively. Equations (8a) and (8b) are illustrated in Bonopera et al. [40]. In specific, the nine test combinations represent the best prestress force determinations among the three test repetitions performed. The chord elastic modulus Eaver of the high strength concrete, for each day of execution of the experiments, was utilized as parameter in the identification process. The corresponding first-order vertical deflections were instead estimated by Equations (4a) and (4b), as similarly reported in Bonopera et al. [40]. Table 1 additionally shows the related percentage errors Δ = (Na − N) / N. In general, poor estimates Na were obtained when prestressing N equal to 617 and 620 kN were assigned (Figure 2a,b). Vice versa, the test combinations with prestressing that induced second-order effects greater than 6.5%, id est, when N ≧ 721 kN, furnished excellent identifications of prestress forces Na. In fact, in this last case, estimation errors were lower, in absolute value, than 6.1%.
Table 1. Prestress force determinations Na based on Equation (8a) (Test 1) and Equation (8b) (Test 2), and corresponding measured parameters for each test day [40]. Copyright © 2018, World Scientific Publishing Co. Pte Ltd. Adapted with permission.
| Test 1-v2(1) Deflections at a Quarter |
Test 2-v4(1) Deflections at the Midspan |
||||||
|---|---|---|---|---|---|---|---|
| Days of Concrete Curing | Eaver | N | F | Na | Δ | Na | Δ |
| (MPa) | (kN) | (kN) | (kN) | (%) | (kN) | (%) | |
| 426 | 34,870 | 620 | 20.2 | 777 | 25.3 | 789 | 27.3 |
| 620 | 22.6 | 857 | 38.2 | 857 | 38.2 | ||
| 617 | 25.0 | 386 | −37.4 | 550 | −10.9 | ||
| 427 | 37,618 | 724 | 20.1 | 729 | 0.7 | 732 | 1.1 |
| 721 | 22.6 | 721 | 0.0 | 761 | 5.5 | ||
| 721 | 25.1 | 715 | −0.8 | 718 | −0.4 | ||
| 433 | 38,791 | 820 | 20.2 | 846 | 3.2 | 823 | 0.4 |
| 820 | 22.9 | 825 | 0.6 | 825 | 0.6 | ||
| 820 | 25.1 | 824 | 0.5 | 870 | 6.1 | ||
Sensitivity analyses were elaborated for the prestress force determinations based on Equations (8a) and (8b). The vertical deflections v2(1) and v4(1), calculated with 0.01 mm in accuracy by Equations (3a) and (3b) reported in Bonopera et al. [40], and parameter Ψ were modified to generate possible experimental errors. In detail, deflections v2(1), v4(1), and Ψ were alternatively multiplied by 0.99 and 1.01 to reproduce 14 combinations of simulated values for nine different assumed prestress forces N. The average value of the applied vertical loads, Faver = 22.6 kN (Figure 2b), was taken into account in the manipulations. Figure 4 depicts a comparison between the worst determined Na and assumed values N conducted using vertical deflections v2(1) and v4(1), both of which yielded a constant error of about ±107 kN. Based on all the results obtained, a favorable correspondence between analytical N and experimental determinations of prestress force Na was found when midspan deflections v4(1) were taken into account.
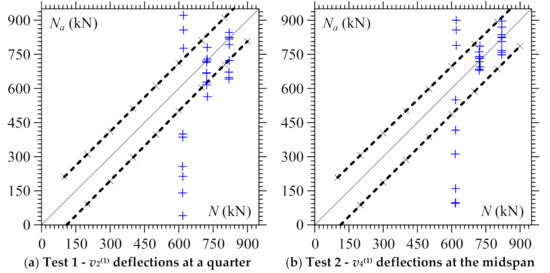
Figure 4. Prestress force determinations Na based on (a) Equation (8a) (Test 1) and (b) Equation (8b) (Test 2). Symbols + refer to the comparison between determined Na and measured values of prestress force N for all the 27 test combinations. The dashed lines with symbol × represent the sensitivity analyses.
A state-of-the-art review of some important research works conducted worldwide on determining prestress losses in PC girders allowed to analyze various information and trace future developments. Some references affirm that a variation in prestress force does not significantly affect the vibration responses of PC girders. Accordingly, this makes uncertain the use of natural frequencies as appropriate parameters for prestress loss determinations. Vice versa, most of laboratory works show a slight increment in the eigenfrequencies under the increase in prestress force. This behavior is related to the concrete mechanics, and is a main consequence of the effect of crack and microcrack closure along PC girders. However, vibration-based identification methods require an accurate selection of the mode shape because different natural frequencies provide varying degrees of accuracy in prestress force evaluations.
By considering these characteristics, the manuscript focused then on the static NDT method preliminary proposed by Bonopera et al. [40] through laboratory simulations on an uncracked PC beam specimen. The procedure can accurately and instantaneously determine the effective prestress force using vertical deflection measurements, of 0.01 mm in accuracy, under actual ambient conditions [46][47]. The precision of estimation improved when the PC beam was subjected to a high prestress force and, moreover, when midspan deflections were taken into account. Information regarding the flexural rigidity of a PC girder under investigation are also necessary. With regards, an average value of the chord elastic modulus, of 1 MPa in accuracy, must be estimated by compression tests on a set of concrete cores, drilled along its span, at the time of deflection measurements. Besides, the static NDT method does not require any direct measure of the tension force in the tendon and, mostly, in contrast to dynamic NDT ones, does not request selecting experimental data for use in the algorithms (Table 5).
Table 5. Characteristics of the static NDT method preliminary proposed by Bonopera et al. [40] for determining prestress losses in PC girders.
| Advantages | Disadvantages |
|---|---|
| (1) Precise determinations by vertical deflection measurements of 0.01 mm in accuracy | (1) Determination of the concrete elastic modulus by compression tests on a set of drilled cores |
| (2) No requirement of direct measure of the tension force in the tendon | (2) Vertical deflections, of 0.01 mm in accuracy, are not always easy to measure in situ |
| (3) No requirement of any selecting experimental data | |
| (4) Determinations take into account the combined effects of tendon relaxation, concrete creep and shrinkage, and parameters of the real environment |
In conclusion, to make the NDT method applicable in situ, further studies should focus on the measurement of vertical deflections induced by bending tests with vehicle loading along PC bridge girders [48][49][50], in which their constraint stiffness should be evaluated with unknown boundary conditions. In fact, static vertical deflections take accurately and instantaneously into account the changes of structural geometry due to prestressing losses on the equilibrium conditions [46][40][47], in turn caused by the combined effects of tendon relaxation, concrete creep and shrinkage, and parameters of real environment of the PC girder as, e.g., temperature and relative humidity [51] (Figure 3a). The FBG-DSM liquid-level system [35][52] is instead an effective measurement device because it can provide bridge deflections over long distances up to 0.01 mm in accuracy (Figure 3b), referred to an absolute point, without any external physical reference and requirements of good environmental conditions, accessibility and visibility in situ.