1000/1000
Hot
Most Recent

Infectious diseases are the primary cause of mortality worldwide. The dangers of infectious disease are compounded with antimicrobial resistance, which remains the greatest concern for human health. Although novel approaches are under investigation, the World Health Organization predicts that by 2050, septicaemia caused by antimicrobial resistant bacteria could result in 10 million deaths per year. One of the main challenges in medical microbiology is to develop novel experimental approaches, which enable a better understanding of bacterial infections and antimicrobial resistance. After the introduction of whole genome sequencing, there was a great improvement in bacterial detection and identification, which also enabled the characterization of virulence factors and antimicrobial resistance genes. Today, the use of in silico experiments jointly with computational and machine learning offer an in depth understanding of systems biology, allowing us to use this knowledge for the prevention, prediction, and control of infectious disease. Herein, the aim of this review is to discuss the latest advances in human health engineering and their applicability in the control of infectious diseases. An in-depth knowledge of host–pathogen–protein interactions, combined with a better understanding of a host's immune response and bacterial fitness, are key determinants for halting infectious diseases and antimicrobial resistance dissemination.
Over the last decade, theoretical and computational biology, combined with open access to biological databases, have presented new opportunities in different areas of the field, such as genomics or evolutionary biology. In the 1970s, bacterial dynamics emerged as its own discipline [1], focusing on the exploration of bacterial population dynamics to gain a better understanding of the bacteria's ability to manipulate, escape, or evade a host's immune response. These traits enable bacteria to transmit and re-infect, providing one of many major questions that modeling tries to address. Other questions that modeling is trying to answer include how bacterial populations evolve under antibiotic pressure, what the function of dose-effect is in the outcome of infection, and what risk factors are associated with epidemics. In addition, models are great tools for the generation of predictions that can be later tested in the laboratory, and in this context, computational (in silico) models combined with systems biology aid clinical microbiology.
Systems Biology started to be developed before World War II, with researchers such as Ludwig von Bertalanffy and, more recently, Mihajlo Mesarovic [2][3], under "the understanding that the whole is greater than the sum of the parts" [4]. The increase in this field was prompted by improvements of functional genomics [5][6], the completion of the human genome project, and the development of high-throughput technologies.
Systems biology intends to unravel the interactions between components of biological systems, as well as the dynamics of interactions, and the changes in systems (inter- and intra- species), by using -omics tools [7]. It is important to consider that systems biology comprises several disciplines, such as biological computing and mathematical biology.
One of the applications of in silico biological data is computational systems biology [8], which uses computational techniques to develop algorithms, networks, and complex connections for cellular and biological processes [9]. In the infectious disease field, the use of these tools is mostly applied to diagnosis, treatment, and prevention.
In summary, mathematical models and computer simulations are mainly utilized to predict changes in systems caused by different environmental conditions. The modelling of infectious diseases [10] is helping us better understand the dynamics of host–pathogen interactions [11], and how the immune response can be orchestrated to differentially respond to inter- and intra-bacterial species interactions. Moreover, computational engineering enables us to predict the evolution or adaptation of bacteria to new environments, including the acquisition of resistance [12] to any given antibiotic.
In addition, protein–ligand docking [13] is assisting in the generation of predictions that aim to understand, in depth, the effects of the position and orientation of a ligand when it is bound to a protein receptor or enzyme and how that position affects the overall efficiency of drugs [14]. This area of study also enables the molecular study of host–pathogen interactions [15][16]. Targeted chemical cross-linking (TX)—mass spectrometry (MS) or TX-MS is a new concept that integrates the complex networks with the modelling of quaternary protein structures [16] (Figure 1).
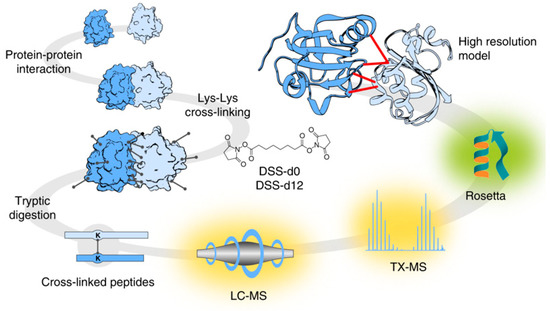
Figure 1. Targeted cross-linking procedure for targeted chemical cross-linking mass spectrometry (TX-MS). Firstly, Protein-Protein Interactions (PPIs) were chemically cross-linked with heavy/light disuccinimidyl suberate (DSS) to further digest the complex PPI cross-linkers. The digested peptide signals were targeted and extracted from Liquid Chromatography (LC)-MS data. The chemically complex cross-linked elements were subjected to MS analysis and subsequently modelled to generate tertiary structures, which were docked to produce a compendium of possible quaternary structure models. For identification of the candidate cross-linked peptides, the authors proposed the use of a guide for the molecular docking of crystal structures of the targeted proteins. This research was originally published in Nature Communications. Hauri et al. Rapid determination of quaternary protein structures in complex biological samples. Nat Commun. 2019 Jan 14; 10(1):192© Copyright Clearance Center's. Reprint from [16].
Epidemiology has been considered the gold standard for investigating diseases' dynamics in varied populations, focusing mainly on the distribution and determinants of disease, to better prevent and control these diseases. Moreover, epidemiology could be considered the first mathematical model applied to the prevention and control of diseases [17]. Epidemic mathematical models have usually been applied to the prediction of outbreaks, epidemics, and transmission, as well as the resurgence of infectious disease [18]. Guidelines and vaccination programmes have been established to prevent and control transmission. Although these first epidemiological models were "static" and representative of neither different social or geographical spaces, nor their evolution over time [17][19], they have served as a model to develop dynamic models that evolve over time (Figure 2).
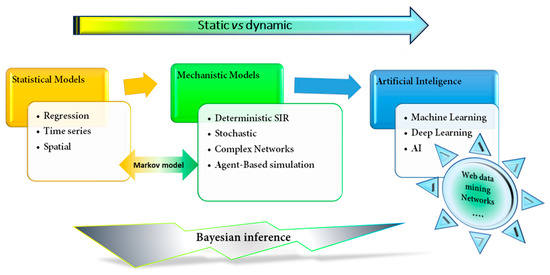
Figure 2. Schematic classification of mathematical models applied to epidemiology and medicine. The figure shows the evolution from a simpler statistical fixed model, such as a regression model, to a more sophisticated and dynamic learning machine or artificial intelligence models. SIR, Susceptible-Infection-Recover.
Bayesian models are based on dynamic probabilistic models, in which a "theorem" describes the probability of any event supported by prior knowledge related to that particular event. The variables are random, and uncertainty can be measured [20]. The applicability of Bayesian models [21], networks [22][23][24], or successful combinations [25], e.g., with gaussian variables [26], is too broad. Certainly, Bayesian methods are more difficult to implement than traditional methods, especially in epidemiology and infection diseases [27]. However, they have been applied in malaria studies [28], to evaluate interventions applied to prevent human immunodeficiency virus (HIV) infection and its collateral risk [29], as well as to evaluate the population dynamics of HIV [30].
Epidemiology (or non-epidemic) models are based on different statistical mathematical models, such as (i) regression, mainly used to detect outbreaks [31], as well as (ii) the autoregressive integrated moving average model, ARIMA, and seasonal SARIMA, both used to predict outbreaks and risk factors [32][33]. Currently, more complex models are gainging popularity, including [34] (iii) models based on a time series, which are more useful in antimicrobial studies to unravel trends [35], (iv) methods including cumulative sum and an exponentially weighted moving average (for example, in the ARIBACA project, were this model was implemented to detect and forecast selected Caribbean diseases, such as dengue [36]), and (v) spatial models, which are more sophisticated, including place-specific models requiring multivariate techniques to model the spatial heterogeneity of all the infection´s covariates [37].
Mathematical or mechanist models are more complex state-space models based on compartments (S = susceptible, E = exposed, and I = infectious and recovered populations). The compartmental or deterministic approach treats each different status of an epidemic as a different sub-population or compartment of a population [38]. The stochastic approach takes random variables into consideration. Susceptible-Infection-Recover (SIR) compartments and derivatives models are mainly used for predictions about the spread of infectious diseases [39], vaccination impact [40], or both [41][42]. Importantly, population dynamics are inexorably subjected to environmental background and natural phenomena, and rather than following random oscillations, they strictly follow deterministic laws. The stochastic or random SIR model has the advantage of introducing "the random or the chance" as a variable [43]. Then, stochastic models can more realistically predict epidemics [44], vaccination impact on herd immunity [45], or the dynamics of protein–protein interactions (PPIs) during infections [46]. Certainly, increasing the complexity and number of variables allows for more realistic predictions that enable us to extrapolate results to real situations. The models proposed by Barnard et al. [47] and Sabini et al. [48] accurately predict epidemics and their spread.
Finally, in the realm of artificial intelligence (AI) and machine learning systems, the studies in [49][50] provide a wide range of novel approaches that are applicable to system biology [51][52] or can be directly used in immunology [53] and the study of infectious disease, for prevention [54] or diagnosis [55][56]. The great similarity between AI and machine learning makes it difficult to separate the two, but in principle, AI aims to function as a human brain, working first on the acquisition of knowledge to then solve problems; this process aims to increase the rate of success and not accuracy. On the contrary, machine learning studies the use of big data to make an informed decision in order to maximize performance. Deep learning is an improved subset of machine learning. The Support Vector Machine [57] and delta bitscore DeltaBS [58] are examples of machine learning applied to a biological system, which enable us to predict the adaptive phenotype of a new host-niche and its probability to develop severe disease. The Support Vector Machine generates a probability, based on assigned scores for each isolate, creating a unique measure of host specificity, to indicate which animals may more easily exchange specific isolates [57][58]. DeltaBS is a training variable that allows the estimation of combined effects on gene function. This model allows the identification of biological mechanisms for adaptation, and the detection of new emerging lineages (by searching recurrent patterns of mutation accumulation) by recognizing novel mutations linked to the same underlying shift [58].
The mammalian immune system is a sophisticated, complex, and well-orchestrated network of cells and antimicrobial molecules operating at different levels to protect it against disease [59][60][61]. Initially, the immune response is innately effective against "new threats". The adaptive immunity responsible for the memory response includes cellular and humoral immune responses. Unfortunately, successful pathogens have developed subversive strategies to exploit, modulate, and/or evade immune control and clearance [59], including evolutionarily optimized protein structures that bind with high specificity to protein-like hosts [62]. In addition, the immune response is highly specific to host and pathogen, hence why everyone has a unique immune system and will respond differently to immune challenges, such as infection or sepsis.
Over this century, the great advances and innovations in computational methods have contributed to a comprehensive and deeper understanding of biologically complex systems and host–pathogen interactions [7]. These new approaches allow us to understand the nuances of these specific interactions [6][9]. Meanwhile, new strategies are developing animal models to better understand and confirm the host immune response against bacterial infections [7][10].
Antimicrobial resistance (AMR) is a major public health concern, and at present, some bacterial infections are untreatable (Figure 3). There is an imperative need for new antibiotics, and new strategies are desperately needed to fight infectious diseases [63]. Previous research has focused on accurate and early diagnosis to better combat infections [55], while some work has also been done to better identify mechanism of resistance in bacteria, mycobacteria, viruses, and parasites. The consensus is to focus on early detection of the microbe, as well as its possible mechanisms of resistance, in order to provide the necessary antimicrobial treatment and avoid a further increase on AMR [12][64][65].
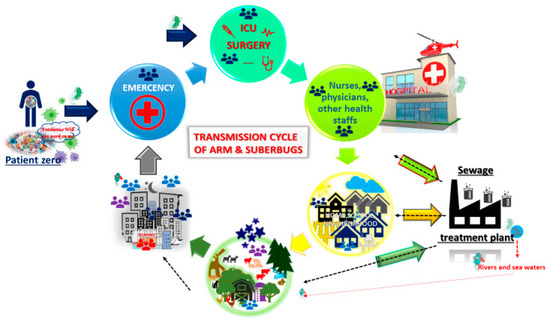
Figure 3. Transmission cycle of antimicrobial resistance (AMR) and/or superbugs. Patient zero (PZ) harbours AMR and/or a superbug. PZ comes to the Hospital because of an infectious disease. The infection is finally overcome with wide-spectrum antibiotics, and PZ leaves the hospital. However, the superbug has been able to spread by fomites, hands, and even directly person to person. Once PZ is at home, he or she is still colonized and harbours the AMR. The superbug then spreads across the neighbourhood, and so on. The superbug ends up at a waste treatment plant. In spite of treatments, the superbug can survive and keep circulating across water for human consumtion. In addition, the residual waste water is spit into rivers or seas, thereby maintaining the ARM and superbugs, and, once more, the cycle starts again. Cartoons are available online [66][67].
AMR is also a complex process that takes place at different levels of bacterial organization. Interactions between microbes and antimicrobials are complex [68], and there are many subtleties to be considered, including colonization, infection, bacterial fitness, and bacterial evolution [12][69][70]. According to environmental conditions, such as antibiotic pressure, bacterial evolution can address independent rates of change and selection [71][72][73]. It is important to highlight that the bacterial mutation rate is faster than the rate in humans, allowing for a rapid evolution that enables adaptation to different threats, as well as immunity [74]. Knowledge of the proteins involved in mechanisms of resistance, as well as the PPI network against antimicrobial pressure, can lead to new ways to improve the development of novel and effective treatment strategies.
Molecular docking [75] focuses on structure-activity studies, screening, and the optimization / modification of novel molecules. This process has promoted novel strategies to emerge in the area of antimicrobial discovery. Zhang et al. [76], for example, combined different machine learning models with molecular docking to select the best strategy, resulting on a novel and highly promising approach. Likewise, TX-MS [16] could be applied to determine bacteria–antibiotic interactions and the disruption of the network under different conditions, in order to unravel the molecular base of mechanisms of resistance. Even so, nothing can predict the AMR ratio, not even the success of a new drug or strategy.
Briefly, statistical models are extensively used to predict the transmission of superbugs and resistant microbes in different settings, e.g., in an intensive care unit (ICU) [77][78]. Most of these models are highly useful to predict and control outbreaks [35]. In addition, dynamics models based on systems instead of compartments [79] are also beneficial to implement in a specific community or region [65]. The stochastic models are the most suitable, when considering variables such as cross-transmission or temporary nursery staff, in the study of outbreaks [80]. Machine learning combined with algorithms and in vitro experiments can help to develop new antimicrobial peptides [81] to predict their activity over different pathogenic microorganisms [82], and at the laboratory level, they can rapidly determine identification and antimicrobial susceptibility [83].
Over the past decades, mathematical models have been developed and improved, further increasing their complexity and better mimicking the biological, chemical, and physiological environments that enable a more robust understanding of host–pathogen PPIs. Mathematical models provide an in silico translational platform, which offers predictions that allow for the investigation of antimicrobial resistance, host–pathogen interactions, and microbial pathogenesis. However, the challenge is still to understand the interactions between host–pathogen–antibiotic microbiota over time, which is the key to overcoming not only septicaemia but all infectious diseases. Deep learning across big data can develop knowledge of each individual immune response to different infections and provide enough information to unravel the molecular mechanism used by bacteria to overcome the host immune response as well as its antimicrobial effect.
Certainly, we are in the initial stages of AI and are still learning how to build more realistic and accurate models. We believe that during the next decade we will have the potential to connect patient diagnosis with treatment using machine learning or AI, which will provide a key finding in translational medicine, as well as tremendous progress towards personalized medicine. However, limitations and disadvantages, such as the non-automatization of the clinical microbiology labs supplying the subjective diagnosis, or the lack of electronic-informatized clinical backgrounds, must be addressed. Overall, the expectation to implement AI is, nowadays, a fact rather than a perspective.