1000/1000
Hot
Most Recent

Double panel structures (DPS) are flat or curved structural designs which consist of two opposite facesheets or panels separated by a core or cavity. The cavity may be any kind of enclosed gasses while the core may be any form of solid materials which can be architecturally designed. DPS have been used in various applications for sound insulation purpose. First, sound incident on the incident facesheet of the DPS, transmitted through the core or cavity and then radiates from the radiating facesheet of the DPS. The ratio of the sound power incident on the incident facesheet to the sound power transmitted through the radiating facesheet is referred as the sound transmission loss of the DPS. The motivation behind the wide industrial application of DPS is owing to their potential characteristics to absorb sound more effectively. Therefore, it is of utmost importance to understand the different geometry and material constituents of the facesheets as well as core/cavity of the DPS. The knowledge of this will help designers and manufacturers to produce the most effective and optimal design of DPS capable of producing very high and desirable sound transmission losses.
The reduction of noise through vibro-acoustic panels has become an interesting area of research in the past few decades. Single and double wall structures have been used for sound insulation purpose and in various applications such as in the aircraft, automotive, marine and building industries [1][2][3][4][5][6][7]. The double panel structures (DPS) have gained popularity over their single panel counterparts owing to their better sound insulation properties and industrial applications over a wide frequency range. Moreover, their vibro-acoustic characteristics can still be improved to give better sound absorbing performance. For example, the DPS have been sandwiched with various interlayers and absorbing materials to improve their sound insulation performance [8][9]. Sandwich structures are low weight and high strength structures which consists of two parallel panels, sheets or laminates bonded to a core or having a cavity between them. The panels which are typically known as the skins or face-sheets can be made from different materials such as metallic, composite or their hybrids. Moreover, the cavity or core between the two face-sheets can be architecturally supported or/and filled with some sound insulation materials [4][8]. In this way, optimal double panel structural design can be adopted for different applications. A very important vibro-acoustic index used to characterize sandwich and composite DPS is the sound transmission loss (STL). This is the ratio of the sound power incident on the incident panel to the sound power transmitted by the radiating panel. During the investigation of vibro-acoustic emission, sound waves impact the incident panel, transmit through the cavity/core and eventually emit from the radiating panel as depicted in Figure 1.
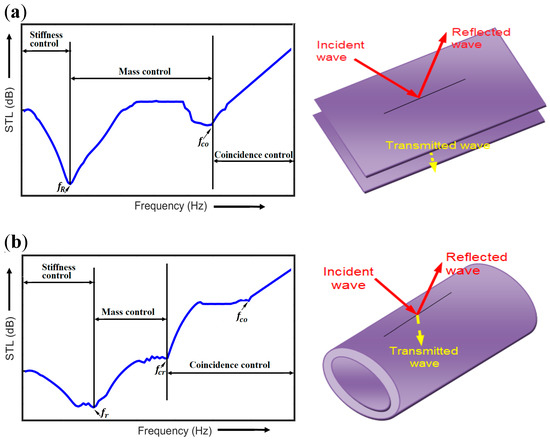
Figure 1. Typical representation of sound transmission loss (STL) curve with different frequency characteristics controlled regions for (a) flat or rectangular double panel structures (DPS) (b) cylindrical or curved DPS.
The STL of sandwich and composite DPS have been studied by a good number of researchers [10][11]. One of their goals is to study the influence of certain parameters on the STL of DPS [12][13]. These vibro-acoustic structures are being improved upon not only to increase their sound insulation efficiency but also to give them excellent mechanical properties with strong capacity to withstand thermal and environmental stresses. There are two types of geometrical shapes of DPS which are commonly investigated. They include the rectangular or flat plate/shell and cylindrical or curved plate/shell as shown in Figure 1. It should be noted that when the thickness of the panel is far less than the lengths of the other two dimensions, the panel is considered a shell or thin-walled structure [14]. These different panel or shell types can be made lightweight for acoustic application. However, in vibro-acoustic applications, weight reduction produces low STL especially in the low frequency region. The reason for this low STL effect follows the so called mass law which states that the noise being transmitted through a material medium is proportional to its thickness, density and frequency [15]. The challenge, therefore, in recent times is to design and optimize vibro-acoustic DPS that reduce sound more effectively at very low frequency with low density materials. Inspired by this challenge, aeroelastic, viscoelastic and poroelastic materials have been introduced in the core [16][17][18]; and materials with orthotropic or anisotropic properties have been used as face-sheets [19][20]. Few authors have attempted to improve the transmission loss of DPS at low frequency by attaching mass on the panel [21], in between the two panels [22] and using metamaterials [23][24] on the face-sheets of DPS. A recent research conducted by Sui et al. [25] was based on the use of acoustic metamaterials to obtain high STL of DPS at low frequency.
To analyze fully the noise transmitted during vibro-acoustic excitation of DPS, the STL curve has to be clearly understood. The curve shows the various frequency regions and also gives the actual characteristics of the material to absorb sound. In the STL characteristics curve, several dip frequencies can be observed which may include the resonance frequency (fR), mass–air–mass frequency (fMAM), ring frequency (fr), critical frequency (fcr) and coincidence frequency (fco) as expressed by their formulas in Table 1. For unbounded panels with enclosed air cavity, the first dip of the STL curve corresponds to the mass-air-mass frequency (fMAM). Resonance frequencies are commonly observed with flat or rectangular DPS while ring and critical frequencies are characteristics of cylindrical or curved DPS [26]. Coincidence frequencies are common to all considered DPS cases. For flat plate or shell, the resonance frequency (fR) is the first frequency which occurs when the frequency of the vibrating structure reaches its natural frequency. As stated, this frequency is missing in cylindrical shells, rather a ring frequency (fr) which is the first transition frequency is observed as shown in Figure 1b. At this frequency, the longitudinal wavelength equals the circumference of the structural element [27]. The next observed frequency for the cylindrical or curved shell is the critical frequency (fcr). This is the dip frequency where the circumferential wave number and mode order divided by the radius of shell are equal. The expressions of the critical dip frequency of DPS have been given by Blaise et al. [26]. The dip frequency that is common to flat, cylindrical or curved DPS is the coincidence frequency (fco). At this frequency, the wavelength of the trace velocity of the acoustic wave becomes equal to the bending wave velocity of the DPS. Moreover, the coincident frequency approaches the critical frequency as the incident angle (θ) becomes 90 degrees. Table 1 gives the formulas used for calculating these frequencies at different regions. From Table 1, the symbols E, Rs, ρ and ν represent Young’s modulus, radius of the cylindrical shell, density and Poisson ratio, respectively. While hs and c represent the thickness of the cylindrical shells and velocity of flow in the medium, respectively; the symbols k, h, A, mk, ms1, ms2 and H are stiffness, thickness, area of the piezoelectric patch of resonator, mass of the equivalent spring, surface mass densities of the two panels and distance between the two panels, respectively. Also, these frequencies are key indicators typically used by researchers to analyze the vibro-acoustic response of double panels or shell structures [28][29][30].
Table 1. Formulas and definitions of frequency terms commonly used at different regions of sound transmission loss (STL) curves.
Reference: Resonance [12]; Mass-air-mass resonance [31][32]; Ring [33][34]; Critical [30][34]; Coincidence [34][35].
Several studies of transmission loss for sandwich and composite DPS have revealed various important regions [33]. However, the transmission loss characteristics curve can be generally divided into three regions—the stiffness controlled region, the mass controlled region and the coincidence controlled region [34][36][37][38][39][40] as depicted in Figure 1. From the figures, the stiffness controlled region emanating from the origin to the first resonance for flat plate or the transition resonance for cylindrical or curved shell, is seen as a falling STL curve in the low frequency region. The region of the curve between resonance frequency and coincidence frequency for flat or rectangular structure is the mass controlled region. This curve is typically seen as a rising curve and is controlled by the mass law [41]. In some special cases, for flat or rectangular structure, as the stiffness of the material decreases, a damping controlled region could be observed [42][43]. Moreover, the mass-controlled region is also observed by the cylindrical or curved structures but they are within the ring frequency and critical frequency regime as depicted in Figure 1b. The coincidence controlled region is the region of the curve after the coincidence frequency for most flat or rectangular structure. However, this region begins from for cylindrical or curved structures. It could arise when there is a coincidence between the structural and acoustic wavelengths. Apart from these common controlled regions, some authors have described other kind of regions which may exist between the stiffness controlled and the mass controlled regions. For examples, between these regions, Zhang and Du [44] described the STL of a flat plate to have a few-mode region while Oliazadeh and Farshidianfar [45] described a resonance controlled region of the STL for cylindrical shells.
Sandwich structures are generally made of two face panels and low density cores. The materials of the sandwich panels can be made from metals or composites and the cores for example can be made from poroelastic materials such as honeycomb or foams [46][47]. The properties of the sandwich structures that have attracted its usage in vibro-acoustic application are their high strength and flexural stiffness.
Double panels with enclosed air cavity may be regarded as the simplest or pseudo form of an equivalent sandwich structures for vibro-acoustic application. Transmission loss results obtained from this equivalent double panel structure can be used as a basis for comparison of the STL results obtained from sandwich core structures. The enclosed air cavity between the two panels allows the transmission of sounds from one panel to the other and has been described to be equivalent to a mechanical spring [48]. It is worthwhile to note that the use of mechanical spring between the panels of the enclosed air cavity or the mass–air–mass (MAM) region of the DPS, reduces their STL especially in the mid and high frequency region. However, introducing a damper to the mechanical spring can increase the STL. Moreover, the first vibration mode of mass–spring–damper (MSD) attached at the center of the air cavity DPS can be seen to be different from that without spring and damper as shown in Figure 2.
Figure 2 (a) first vibration mode of mass–air–mass (MAM) system (b) first vibration mode of mass–spring–damper (MSD) system
The core of sandwich structure not only ensures transmission of sounds to the panel but also acts as a mechanical support for the system. Sandwich DPS can be made with different core supports which may include honeycomb [49][50], foam [51][52], corrugated core [53] or pyramidal truss core [54]. Metallic honeycomb core have been widely used in aerospace application [55]. The honeycomb sandwich core provides a bi-directional support for the double panels which in turn gives the entire DPS a high performance to weight advantage. Few studies have revealed the advantage of using honeycomb cores to improve the STL of sandwich structures [56][57][58].
The sandwich core can be stiffened or structured as a lattice truss core. This 3-D lattice truss core sandwich structure is currently applied in aerospace and marine industries owing to their higher specific stiffness, lower density, lower thermal conductivity and better sound insulation properties. The different forms of these sandwich core supports that have been adopted by contemporary researchers to evaluate STL are the octahedral core, tetrahedral core, pyramidal core, and 3D-kagome core [59][60][61].
The use of sandwich composite panels with anisotropic properties has been adduced to give higher STL than those with isotropic ones [62]. Sandwich composite structures are particularly suited in the aerospace industry owing to their ability to protect materials and equipment in the aircraft from external noise that could cause their damage. Apart from the good noise reduction behavior of these structures, they also exhibit higher stiffness, higher strength and lower density than their metallic counterpart. The shape of the composite panels investigated by researchers are typically made flat, cylindrical or curved as previously mentioned. However, no sufficient literature has been found to compare the effect of the different geometrical shapes on the STL of sandwich composite structures.
The influence of various parameters on the STL of flat sandwich composite structures as depicted in Figure 3, has been investigated by a good number of researchers [63][64][65][66][67][68][69][70]. As already stated, the cavity may be enclosed with air or gases and the core may be architecturally designed by using poroelastic material such as foam and truss core as depicted in Figure 3.
Figure 3. Schematic representation of sandwich composite flat panels with different core and cavity types.
Composite cylindrical and curved shells are sandwich double wall structures that have also attracted attention in the aerospace and marine industry. Their practical application has been seen in the construction of sandwich composite fuselage [71]. In the previous paragraph, the flat sandwich composite structures were assumed by researchers to have finite structures. However, in the calculation of the STL for the cylindrical composite shells, they are mostly assumed by researchers to be infinitely long. A good number of contemporary authors have investigated the effects of various parameters on the STL of cylindrical sandwich composite shells. The STL of composite curved shells was also studied by Ghinet et al. [72]. One of the advantages of metallic curved or cylindrical shells over composite curved or cylindrical shells is their higher ring frequency which in turn produces higher STL. Further, another limitation of the composite shells which has affected the lowering of their STL is that their coincidence zone has the proclivity to extend over a wide frequency range than their metallic counterpart. However, insulators, metamaterials and poroelastic materials have been introduced in the cores of composite cylindrical or curved shells to raise their ring frequencies and further improve their STL characteristics.
Functionally graded materials (FGM) are materials whose composition or microstructures are graded and patterned to give specific functions. While the conventional composite laminates have sharp interface between their constituent materials (i.e., as shown in Figure 4b) which makes them susceptible to high stress concentration, the FGM, however, have smooth variation at their interface as shown in Figure 4a. As a result of this, their properties gradually change in the unit cell, therefore, giving them strong bonding and reduced stress concentration [73].
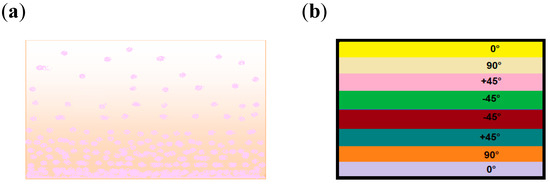
Figure 4. Comparison between (a) functionally graded material with smooth graded variations and (b) composite laminates with sharp interfaces.
Over the years, quite a number of numerical and mathematical models, theories and methods have been developed by researchers to describe vibro-acoustic response and calculation of the STL of sandwich and composite DPS. For example, the DPS with corrugated cores investigated by Bartolozzi et al. [74] was described by using the Timoshenko beam theory for the sandwich panels while the coupling between the core and the faceplate was described using the classical lamination theory.
Statistical Energy Analysis describes the energy flow correlation for the vibration modes of resonating DPS. It has been suitably adopted when dealing with large structures and vibro-acoustic excitation with high frequency response. Different notable authors have used this method to predict the STL of double walls, composite and sandwich structures [75][76][77][78][79].
Transfer Matrix Method (TMM) can be used to model acoustic waves passing through a double wall structure such as the cylindrical wall as described by Parrinello et al. [80]. The calculation is based on the relations between displacements and stresses at the interface of each layer. The method can be used to model multi-layered noise control treatment for example, in functionally graded material and composite laminates. Daneshjou et al. [33] employed this method to estimate the STL of a functionally graded cylinder under subsonic external flow. Two forms of TMM are the impedance matrix model and superposition model. A comparison between these two models on the transmission loss was performed by Hua et al. [81]. It was observed by the authors that the superposition method was better than the impedance matrix method because for the superposition method, matrix assembling was not required for obtaining the transmission loss.
Another type of model employed is the general discrete laminate model (DLM) as described by Ghinet et al. [72] with Ghinet and Atalla [82] combines the attributes of discrete sandwich model and the symmetric laminate model. While the former assumes thin laminate skins and a shear bearing core, the latter assumes each laminate layer thick. The use of DLM permits both the skins and core to have thick laminates such that each laminate layer thickness has smeared features. Moreover, it can handle both the symmetrical and asymmetrical behavior of composite and sandwich shells having thin or thick laminate skins.
Finite element methods have been used to model the vibroacoustic emission of sandwich and composite DPS [32][83]. An improved method—the wave finite element method (WFEM) described by Mace and Mancony [84], Droz et al. [85] and Chronopoulos et al. [86], is a numerical model reduction method which permits the modelling of each cell element rather than modelling the complete structure. The method entails the combination of both the finite element and the periodicity of the structure with the advantage of low computational cost. In recent times, this model was adopted by Yang et al. [87][88] to predict the STL of multi-layered panels with fluid layers. Zergoune et al. [89] also adopted this model recently to model the STL of sandwich structures particularly in the low and medium frequency range. The authors used the DLM and the WSFE model with experimental results to verify and validate, respectively their predicted model.
Periodic structural links when applied appropriately between the sandwich panels are very effective in evaluating the STL at low and mid frequency regions. Various models for periodic structural links have been examined by Legault and Atalla [90]. Moreover, the introduction of porous media or poroelastic materials in between these structural links of sandwich and composite panels can enhance sound reduction in the mid and high frequency regions. Two basic important theories have been used to model these poroelastic materials; they are the Biot’s theory [91][92][93][94] and the equivalent fluid method (EFM) [35][95][96]. While the Biot’s theory assumes an elastic frame in the porous media such that there exist two dilatational or longitudinal (i.e., compressive) waves and one rotational (i.e., shear) wave; the EFM assumes that the porous media is equivalent to a fluid medium having density and bulk modulus. A comparison between these two approaches for fiberglass and foam cores were studied by Panneton and Atalla [97].
A combination of two or more models to predict the STL of sandwich or composite DPS can result into a hybridized model. One possible reason for hybridization is to take care of limitations which could arise from a single model adaptation. For example, Decraene et al. [98] combined the TMM and the hybrid finite element (FE)-SEA models to give a hybridized TMM-SEA model. Other hybrid models which have been investigated are the finite element transfer matrix method (FE-TMM) [99][100] and the patch transfer models [101][102].
As discussed in the previous sections, a good number of researchers have used analytical tools to predict the STL of sandwich and composite double wall structures. Analytical solutions give the exact solution of the physical problem. However, representation of complex configurations using analytical approach may be intractable. Motivated by this challenge, numerical methods such as finite element methods are better suited to model complex scenarios. The numerical solutions are approximation solutions while the exact solutions can be used to verify these approximations. In addition, the numerical approach not only produces interesting results despite the complexity of the structure, it can also be used to virtually validate analytical and experimental results. A number of numerical tools have been utilized to obtain solutions of sound transmission in different vibro-acoustic media. Typical of these tools are the Comsol Multiphysics [103][104][105][106], Ansys Acoustic (ACT) [65][107][108][109] and Abaqus [110][111]. However, the use of Abaqus software for STL solution has been restricted to lower range of frequencies. This is because; it is computationally burdensome especially in the high frequency range [112]. The following sections discuss a combination of STL solutions undertaken by researchers for verification and validation of their research findings.
A very few attempts of using mathematical solution to verify numerical approximations have been carried out by researcher [113][114][115]. Various researchers who modelled the STL through numerical methods also conducted some experiments and the results of the measured data were compared with results from the numerical approximation. To account for complexities like perforations on facesheet/panel and core, a numerical study was performed by Meng et al. [116] and their findings were validated by measured data. Further, Kim et al. [117] numerically predicted the STL of complex extruded panels. They applied the wave number domain numerical method to predict the STL of panels with constant cross-section in one direction. The predicted solutions were compared with measured results and a fair correlation of the two results was observed. A handful of research works on the STL of sandwich and composite structures have been carried out using analytical solutions and these have been validated through experimental measurement [118][119]. Most authors validated their analytical predictions by either performing experiment using the same parametric conditions or by comparing them with the measured data of previous works.
The sound transmission losses (STL) of various types of DPS have been discussed in this review work. The major point is that double panel structures have gained popularity over their single panel counterparts owing to their wider applications and better transmission loss behavior. Different parameters such as geometrical parameters, structural parameters, material parameters and orientated parameters have been investigated by a good number of researchers. These parameters have varied significant influence on the sound transmission loss of DPS. Also, quite a good number of researchers have endeavored to use analytical and experimental methods to model and validate, respectively the STL of flat and cylindrical double panel shells/plates. The analytical procedures give the exact solutions while the measured experimental results give the actual solution of the physical problem. However, a major drawback of these two methods is that complex scenarios which may ensue in practical applications may be intractable. Numerical approaches, for example, finite element approximations are veritable means to addressing this drawback. For this purpose, more numerical procedures are needed not only to handle the complexities of the structure but also to virtually validate results obtained through analytical and experimental methods.
As has been previously mentioned and well reported that increase in the thicknesses and sizes of the composite and sandwich double plates or shells result in the increase in the STL. However, the increased parameters create additional weight and therefore elongate the computational period and final cost of production. While the utilization of lightweight sandwich and composite panels has promising potentials to overcome these drawbacks, however, their STL are mostly enhanced in the low frequency domain or before the mass controlled region. To adequately address these challenges, studies have shown that well defined optimization problems, for example, a multi-objective optimization problem, can be adopted. This solution and other optimization methods can maximize the STL in all frequency domains and equally reduce the weight of the material. However, very few research works have been carried out using different optimization problem procedures. It is therefore expected that more efforts should be channeled in this area because it promises a veritable solution to addressing many of the drawbacks encountered with enhancing the STL of these systems. In addition, with this approach, the design of sandwich and composite double panel structures can be tailored to specific industrial applications for optimal transmission loss results.