Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1 Micromechanical modeling, which is based on structural information, allows the prediction of the elastic and elastic-plastic deformation behavior and, furthermore, to study the dependence of macroscopic properties on individual structural descriptors.
Norbert Huber
 + 2287 word(s) 2287 2020-08-06 11:23:16 |
2 format correct
Catherine Yang
 -23 word(s) 2264 2020-08-20 05:16:36 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Richert, C.; Huber, N. Micromechanical Modeling of Nanoporous Metals. Encyclopedia. Available online: https://encyclopedia.pub/entry/1577 (accessed on 20 April 2024).
Richert C, Huber N. Micromechanical Modeling of Nanoporous Metals. Encyclopedia. Available at: https://encyclopedia.pub/entry/1577. Accessed April 20, 2024.
Richert, Claudia, Norbert Huber. "Micromechanical Modeling of Nanoporous Metals" Encyclopedia, https://encyclopedia.pub/entry/1577 (accessed April 20, 2024).
Richert, C., & Huber, N. (2020, August 10). Micromechanical Modeling of Nanoporous Metals. In Encyclopedia. https://encyclopedia.pub/entry/1577
Richert, Claudia and Norbert Huber. "Micromechanical Modeling of Nanoporous Metals." Encyclopedia. Web. 10 August, 2020.
Micromechanical Modeling of Nanoporous Metals
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ma13153307

Nanoporous metals are characterized by a complex bicontinuous structure, which is similar to open pore foams but typically has a higher relative density. Micromechanical modeling of nanoporous metals consists of the modeling of the complex microstructure and, based on this structural input, the simulation of the mechanical behavior by numerical methods using Molecular Dynamics, Finite Element Methods, or Finite Cell Methods. The microstructure is usually obtained from 3D high-resolution imaging techniques and subsequent image processing. Alternatively, artificial microstructures with sufficient similarity to nanoporous metals can be generated by computational methods. The investigated volume is limited to a Representative Volume Element (RVE), which is small enough for achieving an elastic or elastic-plastic simulation on a computer, but large enough to deliver a reliable result, which is not any more affected by the randomness of individual features within the modeled volume of material and the boundary conditions applied to the RVE. The mechanical simulation predicts the macroscopic deformation behavior that is required to determine the Young's modulus, stress-strain curve as well as further detailed information on defect generation, deformation mechanisms, local stress and strain fields, etc. On the macroscopic level, structural descriptors are combined with predicted mechanical properties to establish structure-properties relationships.

Nanotomography 3D image processing representative volume elements geometrical characterization descriptors MD simulations finite element simulations deformation mechanisms macroscopic mechanical properties structure-properties relationships

1. Introduction

Nanoporous metals made by de-alloying are receiving increasing attention due to their fascinating functional and mechanical properties, which can be controlled via electro-chemo-mechanical coupling through the huge surface inherent in this class of material. A series of reviews document the potential offered by the interface controlled functionality, particularly sensing and actuation [1], electrochemical conversion and storage [2], and bioanalytical and biomedical applications [3]. While originally, the research in this field concentrated on noble elements, such as gold, platinum, or palladium, the range of elements from which nanoporous materials can be produced by electrochemical dealloying has been substantially extended during the last few years with the help of liquid metal dealloying [4]. The different processes allow a design for solid fractions and ligament size as well as certain morphologies that can be modeled by kinetic Monte Carlo simulations or phase field modeling. A review of the characterization of the morphologies and mechanical properties can be found in [1][5][6].

2. Micromechanical Modeling

In many aspects, the micromechanical modeling of nanoporous metals is very similar to the modeling of open pore foams where the methodology is mainly based on FE solid models and FE beam models [7][8][9][10][11]. Elasto-plasticity and deformation localization is investigated using various unit cells, including Gibson–Ashby, simple cubic, reinforced body-centered cubic, body-centered cubic, Kelvin, diamond, and Weaire Phelan [12][13]. Excess volume from the overlap of beam elements connecting in nodes was removed in FE beam models by a modification of the ligament shape [8]. This is sufficient for the correction of the nodal mass for solid fractions of up to 10%. The effect of structural irregularities is studied with random Voronoi foam models, periodic cells with randomly deleted features, or perturbation of the structure [7][11][12][14][15]. An advantage of foams is that they show structural feature sizes in the order of 100 µm, thereby providing better access to all the relevant geometric details via SEM and micro-CT for which ligaments and nodes could be modeled in all geometric details [8][10]. Therefore, compared to nanoporous metals, the characteristics of the ligaments and nodes were incorporated in foam modeling much earlier and there still exists significant knowledge in the foam community that would be worth investigating also for nanoporous metals. For instance, Harb et al. have investigated the energy distributions in aluminum and polymeric foams modeled with different cell structures; they have nicely shown that, in addition to axial bending as the dominant deformation mechanism, other modes play a role, such as shear-torsion or axial torsion [16]. They have found that the contribution of torsion increases with increasing perturbation of the structure. About four years later, the usually unnoticed role of torsion as a relevant deformation mechanism in nanoporous metals was reported in [17][18]. In this sense, the micromechanical modeling of nanoporous gold evolved along two initially disconnected paths, which tend to grow closely together today.

Over more than a decade, the interpretation of experiments in the nanoporous metals community was based exclusively on the Gibson–Ashby scaling laws, which are based on ligament bending as the main deformation mechanism of open pore materials [19]. Until today, important insights are gained with the help of this model, which is robust and simple to use [20][21]. Micromechanical models originating from Gibson–Ashby and other periodic structures are arranged along the left column of figure 1 from bottom to top. Computational groups in the nanoporous metals community used also other methods for RVE generation—phase field methods [22], kinetic Monte Carlo simulations [23], or structures generated by Gaussian random fields [7][24][25]. Each delivers structures with striking similarities to nanoporous metals. Developments based on such microstructures are included together with micromechanical models based on tomography data. For the simulation of the elastic–plastic deformation behavior of a nanoporous metal, molecular dynamics (MD) happen to be the natural choice. Here the open-source code LAMMPS [26]with the EAM potential [27] is widely used. This technique offers numerous advantages over finite element methods (FEM). It incorporates surface effects and finite size effects in a natural way via the chosen potential. However, MD is computationally demanding. For achieving solutions in a reasonable time, the size of the simulation box and the ligament size are typically limited to 100 lattice spacing in edge length. The challenge arises how to bridge the gap from MD simulation of structures with few nm ligament size and limited cell size to ligaments of about 100 nm that can be found in coarsened specimens [28][29]. Here the obvious questions are: How far can we go up with MD and how far can we go down in the scale with continuum FE? What can we learn with each method and how can the results be validated and compared with the experimental findings? How can we overcome limitations that are naturally inherent in experiments and simulations to gain more detailed insights and, at the same time, a better overview of the effects within a big parameter space?

In the following sections, we organize the relevant literature in three sections, where we address the prediction of the macroscopic elastic–plastic deformation behavior, the integration of the effects of surfaces stress and surface energy, and the discussion of the effects of topology on the macroscopic response of the material. The works cover RVEs based on periodic cells as well as works that are mainly based on random microstructures. Both paths contribute pieces of a deeper understanding of the structure–properties relationships.

3. Summary and Future Prospects

From the given overview we can conclude that a micromechanical approach purely based on modeling does not exist. Impressive progress has been made by a close interaction of cutting-edge experimental works, inspiring modeling groups to look into the questions raised with the help of computational tools. In many works with highly original and important contributions to the field, both disciplines are strongly interwoven [30][31][28][32][33][34][35][36][37]. Together with these works, where this interaction results from a continuous long-term progression spanning over several groups in the field, an area is formed which deserves to be named experimentally informed micromechanics. Theoretical works inspire experimentalists, as it was the case for the tension–compression asymmetry predicted in [34]. This effect was experimentally confirmed many years later by Lührs et al. [37]. Furthermore, iterative loops form, as the case for the investigation on topological effects in several papers, such as [20][38][39][40], where we look forward to the future development that may hopefully solve this fascinating puzzle about the exponents.

Our view of the development till date and the arising future perspectives is presented in Figure 1, where the first area is highlighted in blue and the latter red. As a common theme, the set of descriptors for geometrical and mechanical properties is continuously extended and improved in its accuracy through the progress made in the various characterization techniques, image processing software, and modeling methods. Owing to the rapidly increasing resolution, the progress in software development pushed by open source projects and the increase in computational power combined with efficient modeling approaches, we are moving from sparse data to rich data. This allows for the application of novel approaches, such as data reduction, data mining, and machine learning, that support us in our efforts of decoding and generalization of the underlying structure–properties relationship.

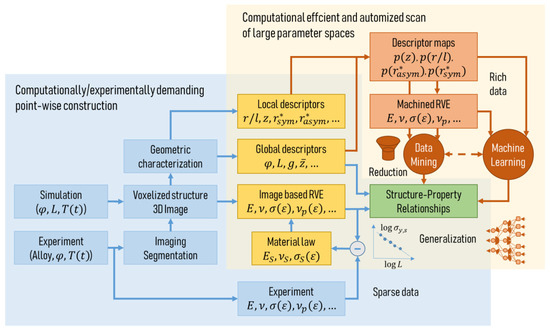
Materials 13 03307 g022 550

Figure 1. Workflow of the microstructure characterization and micromechanical modeling chain for data generation and identification of the structure–properties relationship of nanoporous metals.

Depending on the specific goal, there exist elegant ways of taking a short cut from the experiment to the material properties, as indicated in the lower left part of Figure 1. One example to be mentioned in this context is the work of Zabihzadeh et al. [41]. Samples of nanoporous polycrystalline silver with a porosity of 25–30% and pore sizes in the 200–400 nm range were loaded in tension in situ while observing the sample with a high-energy X-ray beam. After tomographic reconstruction of the microstructure, the deformation behavior of the sample was predicted in an FE simulation and the material law was fitted to the experimentally measured macroscopic stress–strain curve. With this approach, the material behavior of the solid fraction can be obtained in a very robust way. A comparison of the evolution of porosity and local strains measured in situ and from the FE simulation showed a very good agreement for all samples. In addition, having simultaneously global and local information from the experiment, see for example [42], can be very helpful, while the common uncertainties due to error propagation along complex characterization and modeling paths are eliminated. It can be expected that such approaches will serve in the future also for complementing the strategies that will be discussed in the following paragraphs. To transfer this technique to nanoporous metals, the resolution in X-ray imaging needs to be improved to reach a few nm. So far, Larsson et al. have achieved a resolution of 62 nm [43]. For samples with smaller ligament sizes, the existing alternatives FIB-SEM tomography [31][28][44] and TEM tomography [45][46] are much more labor-intensive.

At the same time, the algorithms for image processing need to be further improved, as shown in [47][48]. Currently, valuable information on the morphology is lost or biased due to the nature of the algorithms, causing significant over- or underpredictions by the micromechanical models based on such data. A propagation of such effects can be avoided by using full 3D models in the form of FE solid or FE voxel models, which are, however, computationally very demanding. Independent of the modeling approach, the derived geometric descriptors, serving as independent parameters for the structure–properties relationships, contain still a considerable degree of uncertainty. Further, the flexibility in setting up microstructures with variable morphology and topology using spinodal decomposition [30] or Gaussian random fields [38]] is limited. For a deeper investigation of general parameter spaces, modeling techniques require one to choose both types of descriptors independently. This can, for example, be achieved by combining the approaches of [39] and [48] for defining the connectivity and the shape of individual ligaments, respectively. Furthermore, the generation of the structure needs to be expanded by the incorporation of further descriptors. RVEs based on periodic cells, such as Gibson–Ashby, gyroid, or diamond, allow only for limited integration of randomness by perturbation or random deletion.

In this direction, the first maps of ligament shape distributions already exist [47][49]. Probability densities of the ligament aspect ratio, shape, coordination, and more characteristics could be used for producing a large number of artificial structures that are as close to real samples as far as the descriptors are established and analyzed. This will move artificially generated microstructures closer to the real probability distributions as a requirement for the future work that is highlighted with the reddish color in the upper right corner of Figure 1. Having such a tool in our hands, we will be able to efficiently scan large multidimensional parameter spaces of descriptors and reliably predict the macroscopic mechanical properties for any assumed constitutive law on the level of the single ligament, including effects such as surface energy or actuation by charge injection. We will, then, probably move further from rich data to even big data, allowing for mining and decoding of the fundamental structure–properties relationships of nanoporous metals.

It has been demonstrated in [39] that once we are able to analyze a bigger dataset, we are better able to generalize the gained understanding that can be casted into a simple model. Combining this approach with pioneering simulations on multiaxial loading conditions [36] offers exciting perspectives toward multi-scale simulation schemes that would allow a prediction of the anisotropic deformation behavior with distortion of the yield surface for radial and non-radial loading scenarios.

In view of the new possibilities of machine learning that are, nowadays, readily available and rapidly entering the field of materials science, we shift from computational modeling based on physical equations toward computer approximation of large datasets that ideally integrate experimental as well as machined data [50][51]. This should, however, not be the end. The goal for which we should strive is to utilize the derived approximations to support our understanding of the physics. Once we reach this level, such novel techniques turn into standard computer methods complementing MD and FE simulations. To this end, by combining high complexity with fascinating properties, nanoporous metals represent a perfect candidate providing a vast amount of challenges which need to be addressed by developments in methods, hardware, and software. In return, experimentally informed micromechanics helps to solve the fundamental questions and deepen the knowledge with the help of micromechanically informed experiments.

References

  1. Weissmüller, J.; Sieradzki, K. Dealloyed nanoporous materials with interface-controlled behavior. MRS Bull. 2018, 43, 14–19.
  2. Chen, Q.; Ding, Y.; Chen, M. Nanoporous metal by dealloying for electrochemical energy conversion and storage. MRS Bull. 2018, 43, 43–48.
  3. Şeker, E.; Shih, W.-C.; Stine, K.J. Nanoporous metals by alloy corrosion: Bioanalytical and biomedical applications. MRS Bull. 2018, 43, 49–56.
  4. McCue, I.; Karma, A.; Erlebacher, J. Pattern formation during electrochemical and liquid metal dealloying. MRS Bull. 2018, 43, 27–34.
  5. Lilleodden, E.T.; Voorhees, P.W. On the topological, morphological, and microstructural characterization of nanoporous metals. MRS Bull. 2018, 43, 20–26.
  6. Jin, H.-J.; Weissmüller, J.; Farkas, D. Mechanical response of nanoporous metals: A story of size, surface stress, and severed struts. MRS Bull. 2018, 43, 35–42.
  7. Roberts, A.P.; Garboczi, E.J. Elastic properties of model random three-dimensional open-cell solids. J. Mech. Phys. Solids 2002, 50, 33–55.
  8. Gong, L.; Kyriakides, S.; Jang, W.-Y. Compressive response of open-cell foams. Part I: Morphology and elastic properties. Int. J. Solids Struct. 2005, 42, 1355–1379.
  9. Kanaun, S.; Tkachenko, O. Representative volume element and effective elastic properties of open cell foam materials with random microstructures. JOMMS 2007, 2, 1607–1628.
  10. Jang, W.-Y.; Kraynik, A.M.; Kyriakides, S. On the microstructure of open-cell foams and its effect on elastic properties. Int. J. Solids Struct. 2008, 45, 1845–1875.
  11. Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analyses of 3D regular open cell structures. J. Mater. Sci. 2005, 40, 5859–5866.
  12. Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Numerical simulations of 3D open cell structures – influence of structural irregularities on elasto-plasticity and deformation localization. Int. J. Solids Struct. 2007, 44, 2990–3003.
  13. Nachtrab, S.; Kapfer, S.C.; Arns, C.H.; Madadi, M.; Mecke, K.; Schröder-Turk, G.E. Morphology and linear-elastic moduli of random network solids. Adv. Mater. Weinheim. 2011, 23, 2633–2637.
  14. Gan, Y.X.; Chen, C.; Shen, Y.P. Three-dimensional modeling of the mechanical property of linearly elastic open cell foams. Int. J. Solids Struct. 2005, 42, 6628–6642.
  15. Jang, W.-Y.; Kyriakides, S.; Kraynik, A.M. On the compressive strength of open-cell metal foams with Kelvin and random cell structures. Int. J. Solids Struct. 2010, 47, 2872–2883.
  16. Harb, R.; Taciroglu, E.; Ghoniem, N. Partitioning of elastic energy in open-cell foams under finite deformations. Acta Mater. 2013, 61, 1454–1468.
  17. Jiao, J.; Huber, N. Deformation mechanisms in nanoporous metals: Effect of ligament shape and disorder. Comput. Mater. Sci. 2017, 127, 194–203.
  18. Griffiths, E.; Bargmann, S.; Reddy, B.D. Elastic behaviour at the nanoscale of innovative composites of nanoporous gold and polymer. Extreme Mech. Lett. 2017, 17, 16–23.
  19. Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure & Properties, 1st ed.; Pergamon Press: Oxford, UK, 1988; ISBN 0-08-036607-4.
  20. Xiang, Y.-H.; Liu, L.-Z.; Shao, J.-C.; Jin, H.-J. A universal scaling relationship between the strength and Young’s modulus of dealloyed porous Fe0.80Cr0.20. Acta Mater. 2020, 186, 105–115.
  21. Liu, L.-Z.; Ye, X.-L.; Jin, H.-J. Interpreting anomalous low-strength and low-stiffness of nanoporous gold: Quantification of network connectivity. Acta Mater. 2016, 118, 77–87.
  22. Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267.
  23. Erlebacher, J. Mechanism of coarsening and bubble formation in high-genus nanoporous metals. Phys. Rev. Lett. 2011, 106, 225504.
  24. Roberts, A.P.; Garboczi, E.J. Elastic properties of a tungsten–silver composite by reconstruction and computation. J Mech. Phys. Solids 1999, 47, 2029–2055.
  25. Antman, S.S.; Sirovich, L.; Marsden, J.E.; Wiggins, S.; Torquato, S. Random Heterogeneous Materials; Springer New York: New York, NY, USA, 2002; ISBN 978-1-4757-6357-7.
  26. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19.
  27. Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B Condens. Matter 1986, 33, 7983–7991.
  28. Hu, K.; Ziehmer, M.; Wang, K.; Lilleodden, E.T. Nanoporous gold: 3D structural analyses of representative volumes and their implications on scaling relations of mechanical behaviour. Philos. Mag. 2016, 96, 3322–3335.
  29. Mameka, N.; Wang, K.; Markmann, J.; Lilleodden, E.T.; Weissmüller, J. Nanoporous Gold—Testing Macro-scale Samples to Probe Small-scale Mechanical Behavior. Mater. Res. Lett. 2016, 4, 27–36.
  30. Saane, S.S.R.; Mangipudi, K.R.; Loos, K.U.; de Hosson, J.T.M.; Onck, P.R. Multiscale modeling of charge-induced deformation of nanoporous gold structures. J. Mech. Phys. Solids 2014, 66, 1–15.
  31. Mangipudi, K.R.; Epler, E.; Volkert, C.A. Topology-dependent scaling laws for the stiffness and strength of nanoporous gold. Acta Mater. 2016, 119, 115–122.
  32. Huber, N.; Viswanath, R.N.; Mameka, N.; Markmann, J.; Weißmüller, J. Scaling laws of nanoporous metals under uniaxial compression. Acta Mater. 2014, 67, 252–265.
  33. Crowson, D.A.; Farkas, D.; Corcoran, S.G. Mechanical stability of nanoporous metals with small ligament sizes. Scr. Mater. 2009, 61, 497–499.
  34. Farkas, D.; Caro, A.; Bringa, E.; Crowson, D. Mechanical response of nanoporous gold. Acta Mater. 2013, 61, 3249–3256.
  35. Ngô, B.-N.D.; Stukowski, A.; Mameka, N.; Markmann, J.; Albe, K.; Weissmüller, J. Anomalous compliance and early yielding of nanoporous gold. Acta Mater. 2015, 93, 144–155.
  36. Mangipudi, K.R.; Epler, E.; Volkert, C.A. On the multiaxial yielding and hardness to yield stress relation of nanoporous gold. Scr. Mater. 2018, 146, 150–153.
  37. Lührs, L.; Zandersons, B.; Huber, N.; Weissmüller, J. Plastic Poisson’s Ratio of Nanoporous Metals: A Macroscopic Signature of Tension-Compression Asymmetry at the Nanoscale. Nano Lett. 2017, 17, 6258–6266.
  38. Soyarslan, C.; Bargmann, S.; Pradas, M.; Weissmüller, J. 3D stochastic bicontinuous microstructures: Generation, topology and elasticity. Acta Mater. 2018, 149, 326–340.
  39. Huber, N. Connections Between Topology and Macroscopic Mechanical Properties of Three-Dimensional Open-Pore Materials. Front. Mater. 2018, 5, 5801.
  40. Liu, L.-Z.; Jin, H.-J. Scaling equation for the elastic modulus of nanoporous gold with “fixed” network connectivity. Appl. Phys. Lett. 2017, 110, 211902.
  41. Zabihzadeh, S.; van Petegem, S.; Holler, M.; Diaz, A.; Duarte, L.I.; van Swygenhoven, H. Deformation behavior of nanoporous polycrystalline silver. Part I: Microstructure and mechanical properties. Acta Mater. 2017, 131, 467–474.
  42. Wang, K.; Hartig, C.; Blankenburg, M.; Müller, M.; Günther, R.; Weissmüller, J. Local flow stresses in interpenetrating-phase composites based on nanoporous gold—In situ diffraction. Scr. Mater. 2017, 127, 151–155.
  43. Larsson, E.; Gürsoy, D.; de Carlo, F.; Lilleodden, E.; Storm, M.; Wilde, F.; Hu, K.; Müller, M.; Greving, I. Nanoporous gold: A hierarchical and multiscale 3D test pattern for characterizing X-ray nano-tomography systems. J. Synchrotron Radiat. 2019, 26, 194–204.
  44. Mangipudi, K.R.; Radisch, V.; Holzer, L.; Volkert, C.A. A FIB-nanotomography method for accurate 3D reconstruction of open nanoporous structures. Ultramicroscopy 2016, 163, 38–47.
  45. Rösner, H.; Parida, S.; Kramer, D.; Volkert, C.A.; Weissmüller, J. Reconstructing a Nanoporous Metal in Three Dimensions: An Electron Tomography Study of Dealloyed Gold Leaf. Adv. Eng. Mater. 2007, 9, 535–541.
  46. Fujita, T.; Qian, L.-H.; Inoke, K.; Erlebacher, J.; Chen, M.-W. Three-dimensional morphology of nanoporous gold. Appl. Phys. Lett. 2008, 92, 251902.
  47. Fujita, T.; Qian, L.-H.; Inoke, K.; Erlebacher, J.; Chen, M.-W. Three-dimensional morphology of nanoporous gold. Appl. Phys. Lett. 2008, 92, 251902.
  48. Richert, C.; Odermatt, A.; Huber, N. Computation of Thickness and Mechanical Properties of Interconnected Structures: Accuracy, Deviations, and Approaches for Correction. Front. Mater. 2019, 6, 352.
  49. Pia, G.; Delogu, F. Nanoporous Au: Statistical analysis of morphological features and evaluation of their influence on the elastic deformation behavior by phenomenological modeling. Acta Mater. 2015, 85, 250–260.
  50. Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 443.
  51. Huber, N.; Kalidindi, S.R.; Klusemann, B.; Cyron, C.J. Machine Learning and Data Mining in Materials Science; Frontiers Media SA: Lausanne, Switzerland, 2020; ISBN 9782889636518.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Nanoscience & Nanotechnology
Contributors MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Claudia Richert
,
Norbert Huber
View Times: 404
Revisions: 2 times (View History)
Update Date: 02 May 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback