1000/1000
Hot
Most Recent

Unmanned aerial vehicle (UAV) routing is transitioning from an emerging topic to a growing research area as the 3D flexible utilization of airspace, promogulated by UAVs, is a potential game-changer in solving the urban air mobility challenge by allowing to reshape transportation and logistics in the future. This has revealed a need to classify different types of research and examine the general characteristics of the research area. This research aims to assist in identifying the main topics and emerging research streams and provides a published overview of the current state and contributions to the area of the UAV routing problem (UAVRP) and a general categorization of the vehicle routing problem (VRP) followed by a UAVRP classification with a graphical taxonomy based on the analysis of UAVRP current status. To achieve this, an analysis of the existing research contributions promulgated in this domain is conducted. This analysis is used to identify the current state of UAVRP and the gaps related to the UAVs’ flight dynamics and weather conditions, which significantly influence the fuel consumption of the UAV when modeling the UAVRP.
Unmanned aerial vehicles (UAVs) have been the subject of immense interest in recent years and have developed into a mature technology applied in areas such as defense, search and rescue, agriculture, manufacturing, and environmental surveillance [1][2][3][4]. Without any required alterations to the existing infrastructure, for example, deployment stations on the wall or guiding lines on the floor, UAVs are capable of covering flexible wider areas in the field [5]. However, this advantage comes at a price. To utilize this flexible resource efficiently, there is a need to establish a coordination and monitoring system for the UAV or fleet of UAVs to determine their environment-based route and schedule in a safe, collision-free, and a time-efficient manner [3][6].
While the most common models of UAVs can be identified as quadcopters and the hexacopters, the most common types of UAVs are multi-rotors, fixed-wing, flapping wing, and hybrid systems, where the multi-rotor system is the most popular type of UAVs because it is used for versatile applications and the number of rotors can be in the range of 1 to 12 [7]. The fixed-wing UAV is used inaccurate mapping and monitoring applications due to its long flight endurance and high-altitude operability, which allows covering long distances and carrying equipment such as cameras and sensors [8]. Flapping-wing UAVs are often referred to as Ornithopter that simulates the mechanics of flying birds and insects to generate lift by using semi-rigid articulated wings. These UAVs are mainly used for research purposes due to the improved maneuverability and high flight efficiency when compared to both the multirotor and fixed-wing systems. The hybrid UAVs system is a combination of the multi-rotor and fixed-wing UAVs, and the combination of these two models has boosted its capabilities to allow vertical take-off and landing [8].
Following recent advancements in UAV technology, Amazon, DHL, Federal Express, and other large companies with an interest in package delivery have begun investigating the viability of incorporating UAV-based delivery into their commercial services [8][9]. UAVs have the potential to significantly reduce the cost and time required to deliver materials as, in general, they are less expensive to maintain than traditional delivery vehicles such as trucks and can lower labor costs by performing tasks autonomously [10][11][12][13][14]. To support this emerging area, a new problem category arises, the UAV routing problem (UAVRP). Despite the increasing focus on UAVs and the field’s status as an emerging technology, there is no comprehensive overview of the current state available in terms of the UAVRP characteristics and the methods used to solve UAVRP in the current state.
The main objectives of this paper are to identify the unique characteristics of the UAVRP and present the first overview of the current state of research. This is achieved by analyzing the existing research contributions promulgated in this domain. Based on the analysis, we identify the current state of UAVRP and the challenges in the current state of the general vehicle routing to address the specific nature of the UAVRP. Simultaneously, this paper also provides a published overview of the current state and contributions to the area of the UAVRP. The remainder of the paper is structured as follows: First, a general categorization of the vehicle routing problem (VRP) is presented. An overview of UAVRP based on the analysis of UAVRP current state follows next.
The basis of all routing literature is the VRP, which is a well-studied field and still very much applicable for the advancement of new technology [12][13][14]. VRPs have been applied to solve delivery problems [15], which could appear similar to the UAV routing as a VRP attempts to find the optimal routes for one or more vehicles to deliver commodities to a set of locations [16]. We identify three main dimensions that seem particularly relevant to apply when addressing the UAVRP:
1. The problem type: When classifying routing literature, it can be segregated based on the problem type with an emphasis on the VRP, which has given the major research contributions in the domain of vehicle routing [15][17] and is used as an input for all the routing problems in general.
2. The transportation mode: Routing literature can be partitioned according to the categories of transportation mode, as the characteristics of the modes (such as land, sea, and air) affect the routing methods. Transportation modes have different characteristics in terms of cost, transit time, accessibility, and environmental performance [18]. Compared to other transportation modes, UAVs can be a competitive alternative for delivery and pickup of time-sensitive items, regardless of the ground-level road conditions [19].
3. The degree of automation: The degree of automation in the transportation systems is a dimension as automated systems are discussed in dynamic vehicle routing [20][21], generalized vehicle routing [21], and real-time vehicle routing [22]. Technological advances in the area of UAV have been impressive, and this leads to an increased degree of automation of these systems [23]. In production systems, the majority of research has been focused on automated guided vehicles (AGVs) [24], mobile robot routing [25][26][27][28][29][30][31][32][33][34], or six degrees of freedom aerial robots [34], which are UAVs.
In its simplest form, the VRP addresses the routing of a fleet of homogeneous vehicles to deliver identical packages from a depot to customer locations while minimizing the total travel cost [13]. The VRP definition is that a set of vehicles initially located at a depot are to deliver discrete quantities of goods to a set of customers determining the optimal route used by the set of vehicles when serving the set of customers [13][15][35][36][37][38][39]. The objective is to minimize the overall transportation cost, and the solution of the classical VRP problem is a set of routes that all begin and end in the depot, which satisfies the constraint that all the customers are served only once [13][15][35]. The transportation cost can be improved by reducing the total traveled distance and by reducing the number of required vehicles [13][37][38][39][40][41][42][43][44]. Several sub-categories of VRP exist, addressing a specific set of routing problems [15][35][36]:
These relate to the UAVRP as the different categories of VRP inspire the existing work in UAV routing. In solving the UAVRP, certain studies have used different VRP approaches.
When studying routing literature, it is also apparent that it can be partitioned according to the transportation mode such as land-based, maritime, and air transport. However, the application of VRP is mainly visible in land-based and maritime-based transportation modes as described below, and the UAV routing falls under the domain of air transport along with typical airplanes used in airline industry.
Trucks, delivery vehicles, AGVs, and other land-based transportation modes fall under this category, and much research has been carried out regarding route optimization [48][49]. The VRP can, in this context, typically be described as the problem of designing optimal delivery or collection routes from one or several depots to any number of geographically scattered cities or customers, subject to side constraints [36]. VRP plays a central role in the fields of physical distribution and logistics [42]. In this field, fuel models are seldom considered.
The other relatively well-researched transportation mode is the vessel routing or maritime routing problems [49]. In maritime routing, in contrast to land-based modes of transportation, one generally must consider non-linear fuel-consumption models. The main concern with non-linear fuel-consumption models is that they make the solution of relevant models complicated [49][50]. In this area, one also often encounters network design problems [51] where the aim is to set up cyclical plans [52]. The same is often seen when designing, for example, airline flight schedules [53]. The focus of these is not dynamic routing such as covered by the traditional VRP and of particular relevance to the UAVRP.
This paper also considers the degree of automation of transportation as automation and autonomy play a large role in practical applications of the UAVRP [54][55][56]. Furthermore, they play an increasing role in various modes of transport. Driverless trains are already in operation; the degree of automation in cars is continuously rising, and even the air transport sector is discussing the use of pilotless aircraft [56]. It is observed that certain modes of transportation are fully automated and certain modes are semi-automated [56][57]. Automated guided transport (AGT) systems and AGVs fall under the fully automated modes of transportation and have been subjected to intense study in literature [24][25][27][58][59][60][61][62]. In maritime transport, automated vessel routing has been introduced and unmanned vessels will be the future of maritime transportation [62].
As UAVs flight and navigation tasks are increasingly automated to gain economies-of-scale and speed of operations and support the large-scale operations, UAV routing and execution are evolving from teams of operators managing a single UAV to a single operator managing multiple UAVs as illustrated in Figure 1. The increasing degree of autonomy and automation has created a continuous push for developing methods for managing complex UAV operations. Such systems will naturally require the development of advanced prediction, routing, and scheduling methods and implementation of various systems to support decision-makers in handling the complexity of operations [10][11][12][13]. It is also worth noting that most contributions focus on the VRP characteristics, specific or multimodal transportation modes, and to some degree, on the VRP for automated land-based transportation (typically indoor robotic solutions such as AGVs, mobile robots). While the classical VRP is well-studied, the methods and approaches found within this domain are still very much applicable for the advancement of new technology in the area of UAV operations [12].
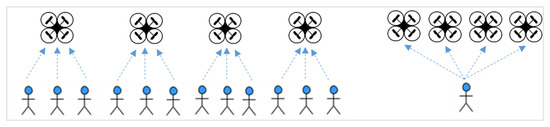
Figure 1. Transitioning from teams of operators managing a single unmanned aerial vehicle (UAV) to a single operator managing multiple UAVs [13].
UAV routing problems involve a huge amount of stochastic information in contrast to VRPs in general, as UAVs should be able to change, adapt, modify, and optimize their routes in real-time. In contrast to general routing problems, several individual objective functions can be used in UAV routing such as reducing individual UAV costs, enhancing its profit, increasing safety in operations, reducing lead time, and increasing the load capacity of the entire system [63][64].
Influencing parameters for UAV routing includes numerous parameters and constraints in contrast to traditional VRP problems. UAVs’ nature is routing and scheduling in 3D environment [65], whereas land- and maritime-based transportation are 2D [66] and in UAV routing, changing weather conditions (wind speed, wind direction, air density) should be considered in solutions. Moreover, UAVs specifications, energy consumption affected by weather conditions, carrying payload of UAVs, and collision avoidance with respect to moving/fixed objects adds more complexity in finding solutions in the domain of UAV routing. All these elements emphasize the significance of UAV routing as it is challenging to develop models considering all the influencing aspects together.
Unlike the traditional routing problems, the UAV routing should address different decision layers in the system architecture (Figure 2), which includes the fleet level where the fleet is managed to provide delivery services using the UAV fleet and the platform level where it focuses on the individual functioning of the UAVs [13]. The current state of research is fragmented as shown in the layers illustrated in Figure 1 and neglects that different types of decisions are addressed at different abstraction levels [13].
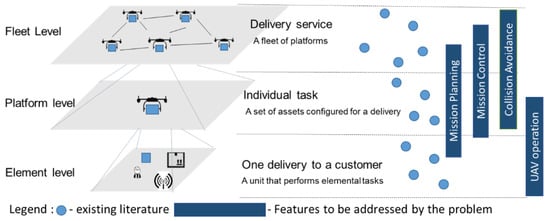
Figure 2. Overall hierarchical representation of the systems related to the UAV routing problem (UAVRP) [13].
Limited contributions have been presented [67][68][69] in the area of UAV routing in 3D environments. What has been accomplished in the field has focused on UAV routing for transporting materials and surveillance [10] without considering the stochastic conditions in weather and non-linear fuel consumption models [9]. Table 1 shows the top seven subject areas in UAV routing literature, where the majority of contributions are seen in engineering and computer science domains.
Table 1. Top seven subject areas.
| Subject Area | No of Papers |
|---|---|
| Engineering | 173 |
| Computer Science | 83 |
| Mathematics | 41 |
| Physics and Astronomy | 25 |
| Social Sciences | 24 |
| Materials Science | 18 |
| Decision Sciences | 14 |
A literature review aims to map and evaluate the body of literature and identify potential research gaps highlighting the limitations of knowledge [70][71]. The search was conducted for the context keyword “UAV routing,” using the “article title, abstract, keywords” search in the Scopus database. Through the exhaustive search, we initially identified 396 papers published in UAV routing, and these papers were analyzed to identify the areas covered in addressing the UAV routing problem.
The first published research we were able to identify on the topic stems from 1998, and this work contains a Reactive Tabu Search (RTS) heuristic within a discrete-event simulation to solve routing problems for unmanned aerial vehicles (UAVs) [72]. The next contribution was in 1999 and proposes a variation of standard VRP that arises in routing UAVs in the presence of terrain obscuration, thus introducing visibility-constrained routing of UAVs [73]. From the timeline presented in Figure 3, it is apparent that the UAV routing theme is gaining increasing attention, especially from 2005 and onward, with a steadily increasing number of publications per year. After the year 2000, an increasing trend is visible with a focus on wireless sensor networking and ad-hoc sensor networking. The top journals and conferences contributing to UAV routing are identified in Figure 4 where publication sources with more than three contributions are included. From Figure 3, The International Society for Optical Engineering Conferences, IEEE Military Communications Conferences, and Journal of Intelligent and Robotic Systems have topped the list with the majority of contributions.
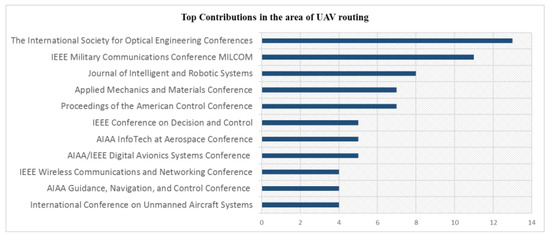
Figure 4. Top journals/conferences contributing to the area of UAV routing [14].
To limit the detailed study of the literature to understand the current state of UAV routing, we chose to focus on all the relevant published journals and the top 10% cited conference papers. This list includes 51 journal papers and 21 conference papers and indicates that the clear majority (70%) of contributions on UAV routing to date have been disseminated through conferences rather than journals.
For the identified 72 main contributions, the keywords have been recorded, and Figure 3 shows a rich image of these and their prevalence. The illustration of the keywords presents the different areas of technologies, industries, and research areas linked to UAV routing. Most commonly used keywords are presented in larger fonts and we can see the various areas linked with UAV routing in Figure 5.

Figure 5. Analysis of keyword frequency in UAV routing.
When considering the published literature both in terms of sources and keywords, it becomes clear that various approaches are used in addressing UAV routing. The contributions’ approaches are inspired primarily by different variants of the VRP and traveling salesman problem (TSP). The difference between TSP and VRP is that TSP considers finding the shortest path that connects an arbitrary number of nodes whose pairwise distances are known [73][74][75].
The most basic form of a VRP can be considered as a direct descendant of TSP [41][76] in which there are one salesman and one fixed depot; the rules are to visit all customers once and only once and end the route at the depot where it started [77]. Many approaches for the VRP were inherited from the huge and successful work done for the solutions of the TSP [39]. This UAVRP is similar to the traditional TSP if the UAV can arrive at or depart from each target only once with the objective of minimizing the total cruise distance [78]. This is relevant in UAV routing if one particular considers sense-and-avoid [79], where the objective is to move to the nearest safe point in a collision-free manner [3][79], or complete autonomy where the UAVs are self-navigating point-by-point [80][81]. The VRP considers a problem similar to the TSP but with a different context, as the VRP considers the problem of delivering goods located at a central depot to customers.
Based on the analysis in the existing literature, VRP approaches used for routing of UAVs can be grouped mainly in a few variants of VRP. These correspond with the general classifications of VRP stated in Section 2. Table 2 categorizes the different VRP approaches used to solve UAV routing. The majority of applied VRP approaches are the general VRP, dynamic VRP, VRP with time windows, and capacitated VRP.
Table 2. Distribution of papers with respect to various domains/approaches used in UAV routing.
| Area/Approach | No of Papers |
|---|---|
| Wireless networks | 24 |
| Scheduling | 8 |
| VRP | 18 |
| TSP | 9 |
| Other | 13 |
Besides VRP approaches, the literature review also identified various other approaches. Chief among these approaches is formulating the problem as a TSP. Table 3 and Table 4 presents an overview of contributions in the literature that utilize the VRP and TSP approaches used in UAV routing. Several contributions use a combination of the variants of both TSP and VRP.
Table 3. Overview of (vehicle routing problem) VRP approaches used in UAV routing.
| Author | Approach | Objective | Experimental Data |
|---|---|---|---|
| [81] Shetty, Sudit, and Nagi, 2008 | General VRP+ multi-vehicle TSP | Maximize the total weighted service to the targets from the homogeneous fleet of UAVs | TSPLIB (http://www.iwr.uni-heidelberg.de/groups/comopt/software) |
| [82] Xingyin Wang, Poikonen, and Golden, 2016 | VRP | Minimize the maximum duration of the routes (i.e., the completion time) | Have considered two problems which have the same set of customers, but different homogeneous fleets |
| [83] Sundar and Rathinam, 2014 | Single VRP | To find a path for the UAV such that each target is visited at least once by the vehicle, the fuel constraint is never violated along the path for the UAV, and the total fuel required by the UAV is a minimum | 50 instances of 10 targets to 25 targets with increments in steps of 5 in each problem size and all the targets are chosen randomly from a square area of 5000 × 5000 units |
| [84] David W. Casbeer, 2011 | VRP with Precedence Constraints | Minimize the total distance traveled by a homogeneous fleet of UAVs | Five UAVs and ten targets placed randomly in the area of responsibility |
| [85] Karaman and Frazzoli, 2008 | VRPTL-VRP with Temporal Logic Specifications | Minimize the relative risk for using a homogeneous fleet of UAVs in the mission. | A scenario with three UAVs, one launch site, two landing sites, and five targets |
| [86] Klein et al., 2013 | Dynamic VRP | Minimize the time required to determine the location of the source | Have conducted a pair of flight tests where they deploy 6 sensors over a 1 km2 region and localize acoustic sources within the area |
| [87] Arsie and Frazzoli, 2008 | Dynamic VRP | Minimize the expected time between the appearance of a target point and the time it is visited by one of the agents | - |
| [88] Murray and Chu, 2015 | VRP+ Flying Sidekick TSP | Minimize the latest time at which either the truck or the UAV returns to the depot | 10 or 20 customers, such that 80%–90% of customers are UAV-eligible according to weight, while the truck and UAV speeds were fixed at 25 miles/h, with the UAV having a flight endurance of 30 min |
| [89] Kinney, Hill, and Moore, 2005 | VRP with Pick-Up and Delivering (VRPPD) + TSP | To find the shortest tour visiting all of the customers | 56 test problems comprising the standard test set of Solomon were used in the testing |
| [74] Guerrero and Bestaoui, 2013 | TSP+ Capacitated VRP (CVRP) | Minimizes the sum of travel time among waypoints | Have considered three 2D and two 3D example scenarios with different waypoints and home waypoints |
| [90] Wen, Zhang, and Wong, 2016 | Capacitated VRP (CVRP) | Minimize the total travel time and fleet size of the homogeneous fleet of UAVs | Have considered nine instances according to different proportions between hot water and blood |
| [75] Savuran and Karakaya, 2016 | Capacitated Mobile Depot VRP (C-MoDVRP) | Maximize the total number of targets visited by the UAV | The simulation tests are conducted using 16 of bench-mark problems from Heidelberg TSP Library (of Heidelberg 1995) |
| [91] Murray and Karwan, 2013 | VRP with Time windows (VRPTW) | Maximize the overall effectiveness of the mission, minimize changes to the initial mission plan, minimize total travel time, and minimize the use of resources, payloads, and “dummy” bases | Test problems are created for a combination of different initial tasks, resources, pop-ups, time window scales, loiter times, and payloads for a battlespace area of size (∼unif(50,400)) × (∼unif(50,400)) |
| [92] Lamont, Slear, and Melendez, 2007 | VRP with Time Windows (VRPTW) | Minimizing cost and risk generally associated with a three-dimensional VRP | Three-element target packages are created along with a grid of real-world terrain and a realistic threat lay down |
| [67] Guerriero, Surace, Loscri, and Natalizio, 2014 | VRP with Soft Time Windows (VRP-STW) | Minimize the total distances traveled by the homogeneous fleet of UAVs, maximize the customer satisfaction and minimize the number of used UAVs | Fleet of 6 homogeneous UAVs in a field of 110 × 80 m2 with different parameters for a sport event |
| [19] Kim, Lim, Cho, and Côté, 2017 | Multi-Depot VRP (MDVRP) | Minimizing the operating cost of a heterogeneous fleet of UAVs and to find the optimal number of UAV center locations | Have considered 9 candidate sites for centers and 40 patients to be served by two types of UAVs |
| [93] Habib, Jamal, and Khan, 2013 | Multiple-Depot VRP (MDVRP) | Minimize the total distances traveled by a homogeneous fleet of UAVs | Have considered 12 instances with different combinations of fleet size and targets (Max fleet size of 5 homogeneous fleets of UAVs and max targets of 101) |
Table 4. Overview of traveling salesman problem (TSP) approaches used in UAV routing.
| Author | Approach | Objective | Experimental Data |
|---|---|---|---|
| [94] Oberlin, Rathinam, and Darbha, 2009 | Heterogeneous, Multiple Depot, Multiple TSP (HMDMTSP) | Minimize the total cost of traveling for the heterogeneous fleet of UAVs | 6 UAVs with a minimum turning radius vary uniformly from 100 to 200 meters and uniformly generated targets [4][40] in a square of area 5 × 5 km2 |
| [77] Liu, Gao, Guang, and Song, 2013 | TSP | Minimize the total traveling time for the homogeneous fleet of UAVs | 6 UAV having cruise speed 100 km/h and maximum distance 200 km |
| [95] Babel, 2016 | The curvature-constrained TSP with obstacles | Minimize the total tour length | One aerial vehicle with a cruise speed of 100 m/s covering an operational area of size 20 km × 20 km |
| [96] Manyam et al., 2016 | Asymmetric TSP | Minimize the total traveling time for homogeneous fleet of UAVs | 2 UAVs in a zone of size 30 × 30 units where targets are located randomly and 50 instances for each problem size with 10–40 targets |
| [97] Furini, Persiani, and Toth, 2016 | Time-Dependent TSP in Controlled Airspace (TDTSPPCA) | Minimize the total traveling time and the holding time over mission waypoints for homogeneous fleet of UAVs | 5 scenarios 10–40 mission waypoints, randomly selected among the navigation points located within a circle having center in Milano Linate and ray of 80 NM |
| [98] Enright and Frazzoli, 2005 | Dynamic Traveling Repairperson Problem (DTRP) | Minimize the expected waiting time between the appearance of a target, and the time it is visited | Simulated with a Single UAV with randomly generated targets |
| [71] Ryan, Bailey, and Moore, |
| 2013 | Multi-vehicle TSP | Maximize the expected target coverage | 21-day simulation of the Sisson’s (1997) [100]notional Nari dataset |
The rest of the papers found in UAV routing, other than VRP and TSP approaches, are mainly in the domain of wireless networks and scheduling. Most of these remaining contributions are related to wireless networks with a focus on contributions in the fields of ad-hoc networks and wireless sensor networks (WSN). Figure 4 presents an overview of these areas. The UAV routing taxonomy covering the four major areas of UAV routing with VRP approaches, UAV routing with TSP approaches, UAV routing in WNS, and UAV routing in scheduling problems are graphically illustrated in Figure 5.
There is a trend to use UAV routing in WSN domain for surveillance, exploring, and monitoring large regions [100][101][102][103][104][105][106][107][108][109][110][111][112][113][114][115]. The recent papers related to UAV routing in various wireless networks are presented in Figure 6. These systems can integrate information from ground with WSN, in atmosphere with the sensors of UAVs and Global Positioning System (GPS). These collaborative systems have been used for large-scale monitoring, increasing mobility, accessibility, and reaction time in case of emergencies [116]. WSNs and ad-hoc networks have been widely used for data collection using UAVs in both outdoor and indoor settings and in numerous application domains, and WSNs have been enhanced with data processing abilities in the direction of on-board intelligence. Physical constraints of energy consumption, communication range and autonomy, data transmission, and processing capabilities have been analyzed literature in the domain of WSN design considerations of UAV routing [116][117][118][119][120].
Figure 6. UAV routing in various wireless networks.
UAV routing in scheduling problems mainly focuses on assigning tasks to UAVs in an approach that efficiently utilizes the fleet of UAVs [121][122][123][124]. UAV routing should be done to have a seamless flight during the operations and the required navigation control is derived from a command, which is provided by a scheduler [122][123][124][125]. Generally, these problems aim at assigning various tasks, and actions such as recharge, hover, and wait-on-ground are assigned to the UAVs at different execution times [4][126][127][128][129]. There is limited literature on UAV routing in the scheduling domain and a summary of related studies that focus on UAV scheduling is presented in Figure 7.
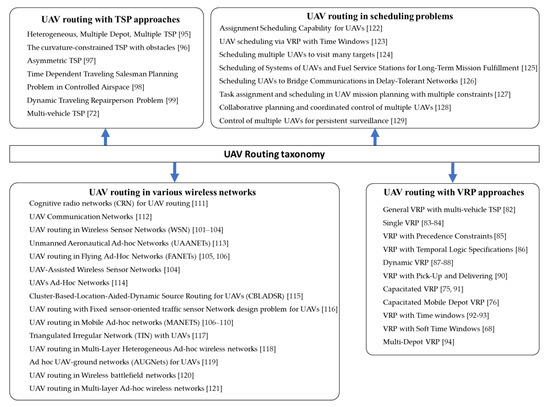
Figure 7. UAV routing taxonomy.
From the overviews of UAV routing literature, the graphical representation of the UAV routing taxonomy is presented in Figure 7. This leads this domain of research to conclude that chief among them is the extensions of VRP and TSP, while the next major contributions are identified in wireless networks as UAV routing is linked with various types of wireless network communication methods.
What is noticeable is that there are some issues in the UAVRP that are unaddressed in the existing literature. Specifically, the authors have identified the following issues that are highly relevant. In outdoor route optimization for UAVs, we must deal with the following stochastic conditions, which have received limited attention in the current state. Stochastic conditions influencing the UAV routing can be identified under weather conditions [13][89][130][131][132], air traffic control [6][13][132][133][134], fuel consumption, and range [135][136][137][138][139][140].
These elements are not encountered in the general VRP or TSP and have some characteristics that can potentially greatly influence the solution strategy for the UAVRP. Ignoring the impact of weather will not provide more realistic solutions as flying with the wind could reduce energy consumption and cold temperatures may adversely affect battery performance [17]. As UAVs have fuel constraints, it may not be possible for a UAV to complete a mission before refueling at one of the depots [84]. Even though these challenges with regard to stochastic conditions and minimizing fuel consumption are studied for some years, they are different regarding the context of this paper as in UAVRP, it is different to typical stochastic VRPs where in UAVRP the routings are done in 3D environment with highly non-linear fuel consumption models and the stochastic behavior is not similar to typical stochastic VRPs. Weather makes the conditions time-dependent as changes in the weather conditions impact the fuel consumption and the flying dynamics of the UAVs. There are various approaches to address the time dependency in routing and, in UAV routing, more focus should be put on the sources of uncertainty and time dependency than on the particular manner in which this stochasticity and time dependencies are addressed.
Weather is a critical feature for UAV routing as it affects the travel speed of the UAV, and the temperature in the atmosphere affects the energy consumption [13][16][140] of batteries used in UAVs. Figure 8 presents the relationships between different factors linked to the energy consumption of UAVs. Weather in various forms is critical for energy consumption as it affects the travel speed of the UAV, and the temperature in the atmosphere affects the energy capacity of batteries used in UAVs. Air density affects energy consumption, but that is a function of humidity, air pressure, and temperature. Flying with the wind could, for example, reduce energy consumption. Cold temperatures may adversely affect battery performance until the batteries warm-up [10][13][141].
The current state of research has not considered the weather factors and ignores the impact of weather on performance [67][83][93]. Interestingly, this seems to add another type of SVRP that should be considered as weather is changing over time in a stochastic manner [133]. Rarely has research focused on considering wind conditions on energy consumption while simultaneously using that information in routing of UAVs [13][136][138].
Many rules and regulations govern the movement of objects in the airspace. These lead to blocking and opening of flying zones [6]. Even though air traffic control has a significant impact on designing and implementing routes for UAVs, none of the current VRP approaches to solve UAV routing has considered this due to its complex nature. Countries have established systems for notifying blocks of airspace where particular limitations are placed on the flight of all types of UAVs. Such areas are typically either: Prohibited Areas, Restricted Areas, or Danger Areas such as military ranges. Other airspaces may have temporary restrictions imposed at specific times, either as a result of a longer-term pre-planned event or in reaction to a short notice occurrence, such as an emergency incident. Permanent Prohibited, Restricted, or Danger areas are marked on aviation ‘Visual Flight Rules’ (VFR) flight charts (maps), which are readily available for purchase online and proprietary VFR flight-planning and navigation software and apps contain such information in their mapping databases. UAVs around airfields or airports that are designated as ‘protected aerodromes’ are tightly restricted. UAVs of any size must not be flown within the Flight Restriction Zone (FRZ) of a protected aerodrome, without appropriate permission. This information about the restricted or controlled air space is taken as input data and used as constraints in UAV route planning. Furini et al. (2016) [97] uses the Time-dependent TSP in Controlled Airspace (TDTSPPCA), which consists of finding the best order of visit of a UAV over a set of waypoints, aiming at minimizing the operational cost and, at the same time, ensuring a minimum separation with respect to the planned air traffic. However, the technology already exists to build UAVs that can see electronically and avoid other aircraft [130].
From the airline industry we know that the fuel/energy consumption depends on certain factors such as maximum flight distance or the flight time of the UAV could be constrained by gross takeoff weight, empty weight, thrust to weight ratio [81], fuel weight, payload, and the number of battery units [115], thereby giving more emphasis to the criticality of focusing on fuel consumption.
The range of the UAV is also a crucial aspect where the existing literature has not to give attention and the range is not the same as fuel consumption, as the extent of this depends on many other conditions. How far a UAV can travel is described as range, and the range of a UAV is dependent on the amount of energy capacity of the UAV, endurance, flight speed, and aerodynamic performance [138][139]. Endurance for a UAV can be explained at the total time taken during the flight. For an electric fixed-wing aircraft or quadrotor, this is directly related to the capacity of the battery and the amount of current the motor produces to keep the aircraft in the air. There are many other aircraft parameters that determine the endurance for any UAV; however, the range of the UAV heavily depends on UAV dimensions, Weight, and Payload [138][139]. Any entity that is concerned about UAV security should be extremely concerned about the endurance and range capabilities of various types of UAV categories.
In routing algorithms, some studies have either assumed unlimited fuel capacities [134] in UAV routing or not considered the fuel at all in their approaches to solving UAV routing. Certain studies in UAV routing have considered fuel as a constraint [68][83], and introduce a fuel-constrained UAV routing problem (FCURP). This implies that, given a set of targets and depots and a UAV that is initially stationed at one of the depots, a path can be found for the UAV such that each target is visited at least once, the fuel constraint is never violated along the path for the UAV, and the travel cost for the vehicle is a minimum.
Although fuel consumption is typically considered in vessel routing [135], when it comes to UAVs, the fuel consumption models differ from vessels by depending on not only just speed but also weight or type of payload and weather conditions [136]. For vessels, the non-linear aspects are heavily dependent on the speed of the vessel [137]. Even though existing research uses linear approximations [11], we know from the industry that this is not a reasonable approach for UAVs where the weight of the payload is more critical when seen in combination with speed and weather conditions [138][139][140][141] From the airline industry, one can find comparable models for flight—such as available fuel models for multirotor helicopters [142][143]—that indicate that linear approximation of the energy consumption is not applicable for large variations of the payload carried [16].
In general, UAV routing is a novel topic. There has been a very limited number of research contributions published on UAV routing compared to the VRP and vessel routing. This paper identifies different VRP approaches to solve UAV routing, and most of them consist of variants of VRP and TSP. This paper provides a detailed overview of UAV routing literature with a general mathematical formulation for the UAVRP and presents a UAV routing taxonomy covering four areas of VRP-based UAV routing, TSP-based UAV routing, UAV scheduling problems, and UAV routing in wireless networks. The four areas of taxonomy are done considering the common attributes from the literature and the proposed taxonomy is applied to 54 recent papers.
In the majority of the literature on UAV routing the kinematics are neglected and the UAVs’ flight dynamics are neglected or simplified using assumptions. It is worth noting that a UAV’s performance is highly influenced by the payload it is carrying (weight and dimensions) and the weather conditions in which it is operating. Both significantly influence the fuel consumption of the UAV and, thus, they must be included when modeling the UAVRP. Such models will lead to computationally expensive formulations with more realistic solutions. There is seldom research done for a heterogeneous fleet of UAVs due to the complexity and the majority of the existing literature focuses on a homogeneous fleet of UAVs. This problem should be further derived by the non-linearity of the fuel consumption model, and it is also worth noting that the existing literature does give importance to stochastic conditions. Thus, modeling energy consumption must be further investigated by giving more focus to the literature. These models and their integration in the UAVRP seem like particularly relevant avenues of future research and development of efficient frameworks for solving UAVRPs addressing the challenges presented in this study need to be answered.