1000/1000
Hot
Most Recent

The development of computational techniques and computer hardware has an impact the analysis of short-term (fast-changing) processes, such as the impact of a non-contact underwater explosion pressure waves. A theory of underwater explosions, gas bubble formation and pressure waves are presented. The course of the pressure wave in time, and its propagation in the acoustic medium are presented. Entry presents empirical descriptions of non-contact pressure explosion waves.
An explosion can be defined as a rapid increase in volume, and a release of kinetic energy or potential energy. The explosion generates a blast pressure wave or shock wave, high temperature and release of gases, in conjunction with loud and sharp sounds caused by the incidents that are associated with the occurrence of each explosion phenomena [1][2][3]. It is also a process of rapid burning with increasing pressure occurring in fractions of a millisecond [4][5][6][7]. The nature of this process is determined by the dynamic conditions in which the flammable mixture is found, in particular the turbulence of the medium. Pressure waves called the shock wave arising during an explosion in liquids (underwater explosion) or in solids reach up to 8000 m/s in the case of detonation. It is also worth differentiating between other processes that may occur during the initiation of an explosive charge.
Due to the speed of the reaction, a distinction is made between combustion, deflagration and detonation. Normal combustion is a process with a propagation velocity of the order of mm/s, for deflagration they are m/s, and for detonation—km/s [8][9]. After reaching the propagation speed > 1000 m/s, deflagration goes into the so-called low order detonation, and at speeds > 5000 m/s is referred to as high order detonation [10]. The transition of deflagration to detonation is accompanied by a change in mechanism: from a process driven by heat to driven by a shock wave [11]. Deflagration occurs on the surface and in a uniform manner, its driving force is generated heat, and the speed of the process depends on the thermal conductivity of the material [12][13]. The direction of propagation of reaction products is opposite to the direction of reaction propagation (these directions are consistent during detonation). Deflagration of the explosive occurs much more rapidly than the combustion of ordinary combustible material, accompanied by a flame or sparks and clear sound effects. It is the basic explosive transformation of propellants (gunpowder). It can run without air [9][10][11].
The product of the underwater explosion is also overpressure, which, depending on the mass of the load reaches a value of 1 to 10,000 MPa. Before the arrival of the shock wave front, the pressure is equal to the hydrostatic pressure of the liquid. With the arrival of the wave front, the pressure increases rapidly up to a maximum value, called peak positive overpressure. The pressure then drops to its original pressure (Figure 1). The period of further pressure drop and its return to hydrostatic pressure is called the negative phase period. Important parameters of the whole process are the maximum value of overpressure and the area under the function describing the pressure dependence on time during the positive phase. The nature and mechanism of the explosion decide many parameters, which include [14]:
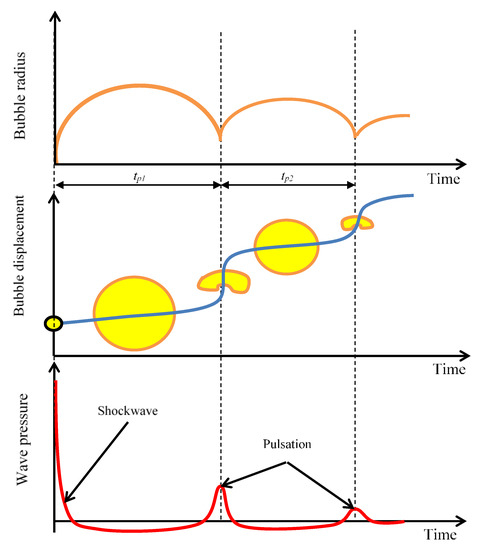
Figure 1. Diagram of the underwater explosion.
The expanding gas bubble acts on the surrounding water layer, creating a spherical shock wave. In the initial phase, shockwave travels at a speed of v ≈ 5000–8000 m/s. Then the water molecules act on the adjacent layers of water, losing their speed and move further at the sound of speed in water, which value reaches about co = 1500 m/s. The pressure wave profile and its value have been described by many researchers. The main of them is R.H. Cole, whose publications form the basis of most research on the subject. The problem is also described by other authors [15][4][16][17][18][19].
Underwater explosion phenomena is wide field of study with deeper aspects to be considered, some of its basic yet most important parameters are hereby summarized and briefly explained, intending to allow the comprehension of fundamental notions of the subject based on a literature survey. The article attempts to collect most of the descriptions of various researchers and implement them for CAE (Computer Aided Engineering) purposes. A similar approach has been proposed in [20]. Table 1 presents formulas necessary to calculate shock waves caused by underwater TNT explosion pressure values and their waveforms. It is also important that the descriptions refer only to the positive pressure pulse wave, excluding the negative pressure phase and pulsation. However, in the methodology of calculations related to the strength analysis of warships [21][22], it is assumed that if a ship withstands the first shock wave, she will be able to survive the subsequent ones caused by pulsations. For this reason, this manuscript refers only to the description of the first pressure wave caused by an underwater explosion. The course of the pressure wave over the years has been studied by various researchers. On the basis of empirical research, they developed formulas (Table 1) for pressure values on the shock wave front pmax and its time course p (t), which depend mainly on:
Table 1. Formulas for calculating pressure values and pressure waveforms given by various authors.