Submitted Successfully!
To reward your contribution, here is a gift for you: A free trial for our video production service.
Thank you for your contribution! You can also upload a video entry or images related to this topic.
Version Summary Created by Modification Content Size Created at Operation
1
Roberto Mantovani
 + 1556 word(s) 1556 2021-06-24 05:29:30 |
2 update layout and reference
Rita Xu
 Meta information modification 1556 2021-07-07 11:14:20 | |
3 update layout
Rita Xu
 Meta information modification 1556 2021-07-07 11:16:10 |

Video Upload Options

Do you have a full video?
Send video materials Upload full video

Confirm

Are you sure to Delete?
Yes No
Cite
If you have any further questions, please contact Encyclopedia Editorial Office.
Mantovani, R. The Rendena Cattle. Encyclopedia. Available online: https://encyclopedia.pub/entry/11772 (accessed on 26 April 2024).
Mantovani R. The Rendena Cattle. Encyclopedia. Available at: https://encyclopedia.pub/entry/11772. Accessed April 26, 2024.
Mantovani, Roberto. "The Rendena Cattle" Encyclopedia, https://encyclopedia.pub/entry/11772 (accessed April 26, 2024).
Mantovani, R. (2021, July 07). The Rendena Cattle. In Encyclopedia. https://encyclopedia.pub/entry/11772
Mantovani, Roberto. "The Rendena Cattle." Encyclopedia. Web. 07 July, 2021.
The Rendena Cattle
Edit
This entry is adapted from the peer-reviewed paper 10.3390/ani11061815

Rendena is a dual-purpose cattle breed indigenous to the North-East of Italy. This breed is included within the “European Federation of Cattle Breeds of the Alpine System” (FERBA), an organization whose main purpose consists in the preservation and promotion of local cattle breeds of the alpine system (http://www.ferba.info, accessed on 20 April 2021).

local cattle breeds genomic prediction ssGBLUP cross-validation

1. Introduction

Rendena is a dual-purpose cattle breed indigenous to the North-East of Italy. This breed is included within the “European Federation of Cattle Breeds of the Alpine System” (FERBA), an organization whose main purpose consists in the preservation and promotion of local cattle breeds of the alpine system (http://www.ferba.info, accessed on 20 April 2021). As is the case with many indigenous breeds, a greater genetic diversity than specialized and cosmopolitan breeds is expected also for the Rendena [1]. This remarkable biodiversity is of great ecological importance and can be a beneficial factor for the survival of the local population. Moreover, traditional breeds such as Rendena provide additional benefits to the local human population such as economic advantages, ecosystem services, and also cultural benefits, such as preservation of cultural heritage and tradition of a specific area [1]. Rendena cattle also shows excellent values for traits concerning fertility and longevity, maintains a median milk production (5000 kg per lactation), and possesses a fairly good beef conformation [2]. Rendena cows are selected for both milk and meat, but with more emphasis on dairy production in the selection index [3], with dairy accounting for 65% and beef traits for 35% [4]. Although beef attitude plays a less important role than milk in the selection index, an increase in the accuracy of the selection for this feature over time could prevent its detriment due to the antagonism with milk production [3]. Estimations of breeding values (EBVs) have until now mostly taken place using classical animal model analysis in Rendena through best linear unbiased predictor (BLUP; [3]) for traits related to milk, meat production, and linear type traits. However, several studies have shown how the use of genomic data can lead to an increase in prediction accuracy compared to using only pedigree information [5].
For a long time, two major limitations to the genomic selection approach on small populations such as Rendena have been the prohibitive cost of genotyping a sufficient number of single nucleotide polymorphisms (SNPs) per individual and the equations for EBVs’ estimation, which were based on a multistep approach [6]. In fact, the drawback of the multistep approach in small populations is the scarce number of genotyped animals with a phenotype to be used as the reference population to ensure a good accuracy of prediction [6]. This is even more noticeable when sex-limited traits are considered [7]. To overcome this problem, methods such as the use of de-regressed proof [8][9] have been developed to allow the inclusion of animals whose only genotype is known, using progeny yield deviation adjusted for mates as a pseudo-phenotype. However, this method presented some biases and lower accuracy whenever animals have few progenies with the phenotype [10][11].
However, in the last few years, both limitations preventing the use of the genomic selection approach in small breeds with limited diffusion such as Rendena have subsided. Firstly, the constant decline in prices of SNP platforms has allowed genomic selection to become much more cost-efficient. Secondly, equations such as the single-step genomic best linear unbiased prediction (ssGBLUP) have been developed and found to be suitable even in small-breed contexts [12]. The ssGBLUP simultaneously evaluates genotyped and non-genotyped animals by substituting the pedigree-based relationship matrix (A) present on BLUP, with a relationship matrix that combines pedigree and genomic information, usually called H [13]. Single-step GBLUP represents a simple alternative to de-regressed proofs. Moreover, ssGBLUP offers the advantage of avoiding double counting contributions, and it implicitly limits the bias of preselection for genotyped animals without the phenotype [14][15][16]. Several studies have shown that ssGBLUP outperformed other methods in different livestock species in the context of genomic selection [17]. On the other hand, ssGBLUP might have its own drawback: the genomic relationship matrix (G) included in a single step assumes that all SNPs explain the same amount of variance [18]. This may be a limit in the presence of traits influenced by many quantitative traits loci (QTL), such as some beef-related traits such as carcass weight and daily gain [19][20]. Indeed, some studies reported that SNP regression equations, in which prior assumption of SNPs’ effect and variance are modeled with different a priori assumptions, outperformed the prediction of ssGBLUP [21]. On this point, Zhang et al. [22] proposed to “relax” the assumption of the G matrix in which all SNPs equally contribute to the genomic variance of the traits by adding specific SNPs weights. These methods are called weighted single-step GBLUP (WssGBLUP), and in a recent study, it has been shown to be effective by increasing the accuracy with respect to ssGBLUP for phenotypes such as those related to the beef attitude [23].

2. Variance Components

Heritability (h2) and genetic and residual correlations estimated using PBLUP are reported in Table 2. All traits presented a medium to high heritability. EUROP was the trait with lowest heritability, 0.304, while ADG and DP showed an h2 of 0.335 and 0.392, respectively. In addition, all traits’ pairs, as expected, presented medium to high genetic and residual correlations. ADG presented a medium-positive genetic correlation with the other two traits (0.38 on average), while DP and EUROP were strongly correlated (0.981) to be considered a unique trait.
Table 1. Mean of genetic (upper diagonal) and residual (lower diagonal) correlations and heritability (diagonal) between traits in the Rendena population, estimated with PBLUP. Numbers in parenthesis are the lower and the upper 95% highest posterior density.
ADG EUROP DP
ADG 0.335
(0.204 ± 0.335)		 0.364
(0.100 ± 0.597)		 0.398
(0.148 ± 0.6315)
EUROP 0.572
(0.660 ± 0.742)		 0.304
(0.174 ± 0.446)		 0.981
(0.962 ± 0.997)
DP 0.613
(0.517 ± 0.702)		 0.792
(0.753 ± 0.836)		 0.392
(0.248 ± 0.541)
ADG = Average daily gain, EUROP = and in vivo fleshiness score CY, DP = in vivo estimate of dressing percentage.
Table 3 reported estimated heritability and genetic and residual correlations using ssGBLUP. In this case, both h2 and correlations had similar results to those estimated with the PBLUP. For what concerns h2, ADG decreased by about 0.02, while EUROP increased by about 0.04 in ssGBLUP as compared to PBLUP. On the other hand, DP remained basically unchanged comparing the two approaches. Correlations presented almost the same values in both analyses, with the only exceptions of the genetic and residual correlations between ADG and EUROP that resulted in an increase in ssGBLUP of about 0.02 and 0.08, respectively.
Table 2. Mean of genetic (upper diagonal) and residual (lower diagonal) correlation and heritability (diagonal) between traits in Rendena population, estimated with ssGBLUP. Numbers in parenthesis are the lower and the upper 95% highest posterior density.
ADG EUROP DP
ADG 0.313
(0.223 ± 0.489)		 0.385
(0.153 ± 0.597)		 0.392
(0.160 ± 0.622)
EUROP 0.651
(0.651 ± 0.718)		 0.345
(0.216 ± 0.487)		 0.985
(0.961 ± 0.999)
CY 0.616
(0.530 ± 0.671)		 0.790
(0.753 ± 0.826)		 0.396
(0.250 ± 0.530)

ADG = Average daily gain, EUROP = and in vivo fleshiness score CY, DP = in vivo estimate of dressing percentage.

3. Weighting Strategies

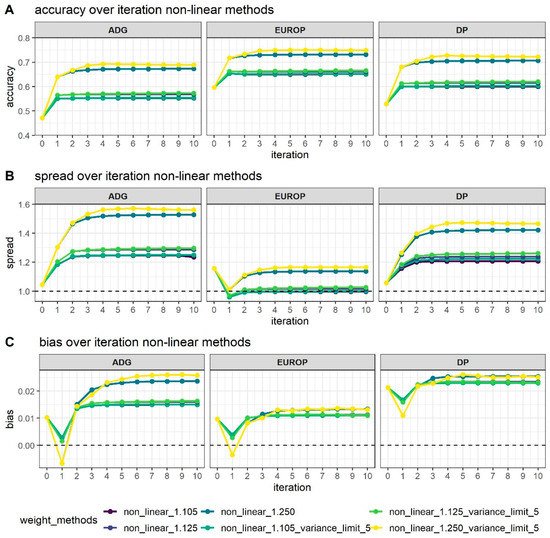
Figure 1 shows how different values of CT and the limitation of SNPs’ variance can affect genomic prediction.
Animals 11 01815 g002 550
Figure 1. Accuracy (A), dispersion (B), and bias corrected by genetic standard deviations (C) of breeding value estimated using different weighting strategies along the 10 iterations process of the algorithm used in WssGBLUP. The dotted line in Graphs B and C represents the expected value.
As expected, higher accuracy (Figure 2A) was reached in the WssGBLUP analyses with the increase of the number of iterations, although in most cases, the asymptote was reached at the second iteration, with the only exception of the CT 1.25 with the limit of maximum variance established at 5, which reached the maximum accuracy after 3–4 iterations. Variance limits did not affect accuracy using a CT of 1.105 or 1.125.
Bias (Figure 1C) followed the same trends in all phenotypes; at first, iteration bias was even lower than with ssGBLUP, but when iterations increased, bias rapidly increased. ADG presented higher biases, even if the difference in magnitude was considered by standardizing values obtained. Even dispersion (spread; Figure 1B) followed the same trends as accuracy with an increase after 2/4 iterations depending mainly on the value attributed to CT. For all traits, as the interactions increased, dispersion departed from the expected value of 1, although for EUROP, the use of CT at 1.125 was maintained steadily close to 1.
In general, higher CT values (that is, greater departures from normality) presented better accuracy but more under-dispersion and biases. When CT changed from 1.105 to 1.125, accuracy increased by 2% in all phenotypes, and a substantial increase in accuracy was observed, moving to a CT value of 1.250 (+20% on average). When the threshold for maximum SNPs variance was raised up to 5, accuracy increased slightly, especially from the third to tenth iteration.
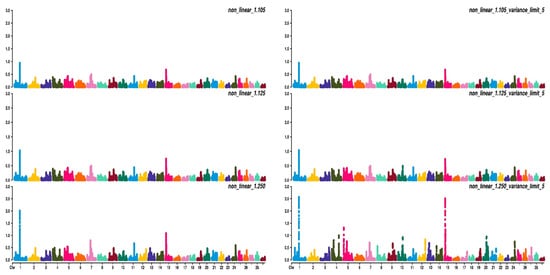
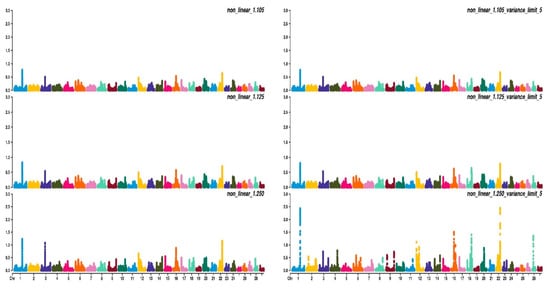
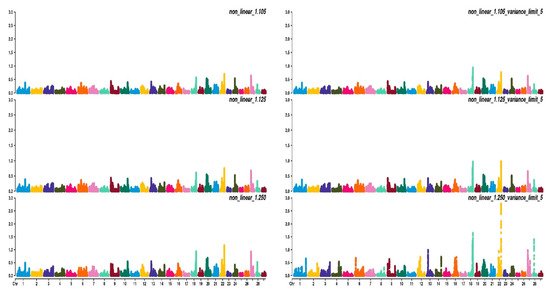
Figure 2, Figure 3 and Figure 4 show the percentage of variance explained by a sliding window of 20 non-overlapping SNPs. These plots show how the different values of CT and limit influenced the shrinkage SNPs. Furthermore, observing the peaks in the Manhattan plots, it can be seen how these traits are potentially controlled by few QTLs. The high peak found on chromosome 22 for EUROP and DP can explain why these traits are highly genetically correlated.
Animals 11 01815 g003 550
Figure 2. Manhattan plots for average daily gain (ADG) using different WssGBLUP strategies in iterations equal to 10; y-axes represent the percentage explained by each SNP. Variance explained was calculated with a sliding window approach.
Animals 11 01815 g004 550
Figure 3. Manhattan plots for fleshiness score (EUROP) using different WssGBLUP strategies in iteration equal to 10; y-axes represent the percentage explained by each SNP. Variance explained was calculated with the sliding window approach.
Animals 11 01815 g005 550
Figure 4. Manhattan plots for dressing percentage (DP) using different WssGBLUP strategies in iterations equal to 10; y-axes represent the percentage explained by each SNP. Variance explained was calculated with the sliding window approach.

References

  1. Schöpke, K.; Swalve, H.H. Review: Opportunities and challenges for small populations of dairy cattle in the era of genomics. Animal 2016, 10, 1050–1060.
  2. Mazza, S.; Guzzo, N.; Sartori, C.; Berry, D.P.; Mantovani, R. Genetic parameters for linear type traits in the Rendena dual-purpose breed. J. Anim. Breed. Genet. 2014, 131, 27–35.
  3. Sartori, C.; Guzzo, N.; Mazza, S.; Mantovani, R. Genetic correlations among milk yield, morphology, performance test traits and somatic cells in dual-purpose Rendena breed. Animal 2018, 12, 906–914.
  4. Guzzo, N.; Sartori, C.; Mantovani, R. Analysis of genetic correlations between beef traits in young bulls and primiparous cows belonging to the dual-purpose Rendena breed. Animal 2019, 13, 694–701.
  5. Zhang, H.; Yin, L.; Wang, M.; Yuan, X.; Liu, X. Factors Affecting the Accuracy of Genomic Selection for Agricultural Economic Traits in Maize, Cattle, and Pig Populations. Front. Genet. 2019, 10, 189.
  6. Blasco, A.; Toro, M.A. A short critical history of the application of genomics to animal breeding. Livest. Sci. 2014, 166, 4–9.
  7. Ibanez-Escriche, N.; Simianer, H. Animal breeding in the genomics era. Anim. Front. 2016, 6, 4.
  8. Van Raden, P.M.; Wiggans, G.R. Derivation, Calculation, and Use of National Animal Model Information. J. Dairy Sci. 1991, 74, 2737–2746.
  9. VanRaden, P.M.; Van Tassell, C.P.; Wiggans, G.R.; Sonstegard, T.S.; Schnabel, R.D.; Taylor, J.F.; Schenkel, F.S. Invited review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 2009, 92, 16–24.
  10. Masuda, Y.; VanRaden, P.M.; Misztal, I.; Lawlor, T.J. Differing genetic trend estimates from traditional and genomic evaluations of genotyped animals as evidence of preselection. J. Dairy Sci. 2018, 101, 5194–5206.
  11. Ma, P.; Lund, M.S.; Nielsen, U.S.; Aamand, G.P.; Su, G. Single-step genomic model improved reliability and reduced the bias of genomic predictions in Danish Jersey. J. Dairy Sci. 2015, 98, 9026–9034.
  12. Aguilar, I.; Misztal, I.; Johnson, D.L.; Legarra, A.; Tsuruta, S.; Lawlor, T.J. Hot topic: A unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score. J. Dairy Sci. 2010, 93, 743–752.
  13. Legarra, A.; Aguilar, I.; Misztal, I. A relationship matrix including full pedigree and genomic information. J. Dairy Sci. 2009, 92, 4656–4663.
  14. Misztal, I.; Lourenco, D.; Legarra, A. Current status of genomic evaluation. J. Anim. Sci. 2020, 98.
  15. Legarra, A.; Christensen, O.F.; Aguilar, I.; Misztal, I. Single Step, a general approach for genomic selection. Livest. Sci. 2014, 166, 54–65.
  16. Ricard, A.; Danvy, S.; Legarra, A. Computation of deregressed proofs for genomic selection when own phenotypes exist with an application in French show-jumping horses. J. Anim. Sci. 2013, 91, 1076–1085.
  17. Misztal, I.; Aggrey, S.E.; Muir, W.M. Experiences with a single-step genome evaluation. Poult. Sci. 2013, 92, 2530–2534.
  18. VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423.
  19. Bedhane, M.; van der Werf, J.; Gondro, C.; Duijvesteijn, N.; Lim, D.; Park, B.; Park, M.N.; Hee, R.S.; Clark, S. Genome-Wide Association Study of Meat Quality Traits in Hanwoo Beef Cattle Using Imputed Whole-Genome Sequence Data. Front. Genet. 2019, 10, 1235.
  20. Fu, L.; Jiang, Y.; Wang, C.; Mei, M.; Zhou, Z.; Jiang, Y.; Song, H.; Ding, X. A Genome-Wide Association Study on Feed Efficiency Related Traits in Landrace Pigs. Front. Genet. 2020, 11, 692.
  21. Mehrban, H.; Naserkheil, M.; Lee, D.H.; Cho, C.; Choi, T.; Park, M.; Ibáñez-Escriche, N. Genomic Prediction Using Alternative Strategies of Weighted Single-Step Genomic BLUP for Yearling Weight and Carcass Traits in Hanwoo Beef Cattle. Genes 2021, 12, 266.
  22. Zhang, X.; Lourenco, D.; Aguilar, I.; Legarra, A.; Misztal, I. Weighting Strategies for Single-Step Genomic BLUP: An Iterative Approach for Accurate Calculation of GEBV and GWAS. Front. Genet. 2016, 7, 151.
  23. Alvarenga, A.B.; Veroneze, R.; Oliveira, H.R.; Marques, D.B.D.; Lopes, P.S.; Silva, F.F.; Brito, L.F. Comparing Alternative Single-Step GBLUP Approaches and Training Population Designs for Genomic Evaluation of Crossbred Animals. Front. Genet. 2020, 11, 263.
More
© Text is available under the terms and conditions of the Creative Commons Attribution (CC BY) license; additional terms may apply. By using this site, you agree to the Terms and Conditions and Privacy Policy.
Upload a video for this entry
Information
Subjects: Agriculture, Dairy & Animal Science
Contributor MDPI registered users' name will be linked to their SciProfiles pages. To register with us, please refer to https://encyclopedia.pub/register :
Roberto Mantovani
View Times: 484
Revisions: 3 times (View History)
Update Date: 07 Jul 2021
Table of Contents
    1000/1000
    Hot Most Recent
    Feedback